题目内容
8.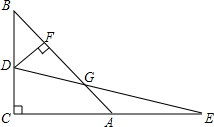 如图,在等腰Rt△ABC中,∠C=90°,动点D从点B出发沿BC方向匀速运动,同时动点E从点A出发沿射线CA方向以相同的速度匀速运动,当点D到达点C时,当点C到达C时,D,E同时停止运动,过点D作DF⊥AB于点F,连接DE交AB于点G,在整个运动过程中(不计点D与B,C重合的情形),线段FG的长度变化情况是( )
如图,在等腰Rt△ABC中,∠C=90°,动点D从点B出发沿BC方向匀速运动,同时动点E从点A出发沿射线CA方向以相同的速度匀速运动,当点D到达点C时,当点C到达C时,D,E同时停止运动,过点D作DF⊥AB于点F,连接DE交AB于点G,在整个运动过程中(不计点D与B,C重合的情形),线段FG的长度变化情况是( )| A. | 一直增大 | B. | 一直不变 | C. | 先减小后增大 | D. | 先增大后减小 |
分析 过E作EH⊥BA交BA的延长线与H,由△ABC是等腰直角三角形,得到∠B=∠BAC=45°,根据DF⊥AB,得到∠BFD=90°,于是得到∠B=∠EAH,推出△BDF≌△EAH,得到EH=DF,证得DG=EG,设BD=x,AC=1,根据勾股定理即可得到结论.
解答  解:过E作EH⊥BA交BA的延长线与H,
解:过E作EH⊥BA交BA的延长线与H,
∵△ABC是等腰直角三角形,
∴∠B=∠BAC=45°,
∵DF⊥AB,
∴∠BFD=90°,
∵∠EAH=∠BAC=45°,
∴∠B=∠EAH,
在△BFD与△EAH中,
$\left\{\begin{array}{l}{∠B=∠EAH}\\{∠BFD=∠H}\\{BD=AE}\end{array}\right.$,
∴△BDF≌△EAH,
∴EH=DF,
在△DFG与△EGH中,
$\left\{\begin{array}{l}{∠DFG=∠H=90°}\\{∠DGF=∠AGE}\\{DF=HE}\end{array}\right.$,
∴△DFG≌△EGH,
∴DG=EG,
设BD=x,AC=1,
∴DE2=(1-x)2+(1+x)2,=2+2x2,DG2=$\frac{1+{x}^{2}}{2}$,
∴FG2=DE2-DG2=$\frac{1}{2}$,
∴FG=$\frac{\sqrt{2}}{2}$,
∴线段FG的长度不变,
故选B.
点评 本题考查了全等三角形的判定和性质,勾股定理等腰直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
16.下列各组式子中,同类项有( )
①-5x2y2与$\frac{2}{3}$x2y2;②42与-10;③3a2b与-4a2bc;④23a2与-3a2b2;⑤3p2q与-qp2.
①-5x2y2与$\frac{2}{3}$x2y2;②42与-10;③3a2b与-4a2bc;④23a2与-3a2b2;⑤3p2q与-qp2.
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
13.关于x的方程x-2a=0的解比关于y的方程3y-a=0的解大5,则a的值是( )
| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
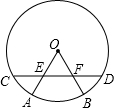 如图,CD是⊙O的弦,$\widehat{AC}$=$\widehat{BD}$,OA,OB分别交CD于点E,F.判断△OEF的形状,并说明理由.
如图,CD是⊙O的弦,$\widehat{AC}$=$\widehat{BD}$,OA,OB分别交CD于点E,F.判断△OEF的形状,并说明理由.