题目内容
4.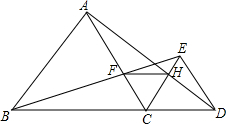 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,①求证:BE=AD;
②求证:CF=CH;
③判断FH与BD的位置关系,并证明.
分析 ①由两三角形为等边三角形,得到两对边相等,且夹角相等,利用SAS得到三角形ACH与三角形BCF全等,利用全等三角形的对应边相等即可的值;
②利用AAS得到三角形ACH与三角形BCF全等,利用全等三角形对应边相等即可得证;
③FH与BD平行,由两边相等且一角为60°的三角形为等边三角形得到三角形FCH为等边三角形,利用等边三角形的性质得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答 证明:①∵△ABC与△ECD都为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE;
②∵△ACD≌△BCE,
∴∠HAC=∠FBC,
∵∠ACB=∠ECD=60°,
∴∠ACH=60°,
在△ACH和△BCF中,
$\left\{\begin{array}{l}{∠ACH=∠BCF=60°}\\{∠HAC=∠FBC}\\{AC=BC}\end{array}\right.$,
∴△ACH≌△BCF(AAS),
∴CF=CH;
③FH∥BD,理由为:
∵CF=CH,且∠FCH=60°,
∴△CFH为等边三角形,
∴∠HFC=∠ACB=60°,
∴FH∥BD.
点评 此题考查了全等三角形的判定与性质,以及等边三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.Rt△ABC中,∠ACB=90°,若∠ACD=50°,则与∠BCD相邻的外角度数是( )
| A. | 130° | B. | 140° | C. | 30° | D. | 40° |
 由四个边长分别为a,b,c的直角三角形拼成一个新的图形.试用两种不同的方法计算这个图形的面积,并说说你发现了什么.
由四个边长分别为a,b,c的直角三角形拼成一个新的图形.试用两种不同的方法计算这个图形的面积,并说说你发现了什么. 已知:如图,AD=CB,AB=DC,BE⊥AC,垂足为E,DF⊥AC,垂足为F.
已知:如图,AD=CB,AB=DC,BE⊥AC,垂足为E,DF⊥AC,垂足为F.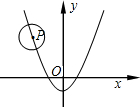 如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).