题目内容
1.用●表示实圆,○表示空心圆,现有若干个实圆与空心圆,按规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○…
问:
(1)第2016个圆,是空心圆(填空心或实心).
(2)第2016个圆之前,包括2016个圆,有672个空心圆.
分析 (1)根据图形可以得到如下规律:●○●●○●●●○为一组,以后反复如此.首先求出2016中有多少组,再由余数来决定最后一个圆是什么颜色;
(2)首先确定组数,然后确定空心圆的个数.
解答 解:(1)由题意可知,前9个圆为本图规律,后边就按这个规律排列.
2016÷9=224,可知2016个圆为空心圆,
(2)2016个圆中,有224×3=672个空心圆.
故答案为:空心,672.
点评 本题考查学生观察,归纳和总结规律的能力,关键是能够发现9个圆是一个循环;

练习册系列答案
相关题目
13.下列方程中,一元二次方程是( )
| A. | ${x^2}+\frac{1}{x^2}$=0 | B. | (x-1)x=1 | C. | ax2+bx=0 | D. | x2-xy-y2=0 |
11.已知函数y=3x2-6x+k(k为常数)图象经过点A(2,y1),B(3,y2),C(4,y3),则有( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |
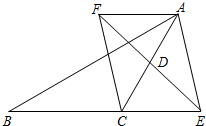 如图,在△ABC中,AC=BC,∠BAC=30°,D是EF的中点,E是线段BC延长线上一点,过点A作AF∥BE,与线段ED的延长线交于点F,连结AE、CF.
如图,在△ABC中,AC=BC,∠BAC=30°,D是EF的中点,E是线段BC延长线上一点,过点A作AF∥BE,与线段ED的延长线交于点F,连结AE、CF.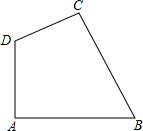 如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.
如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.