题目内容
8.计算:(1)(ab2)2•(-a3b)3÷(-5ab);
(2)(2x-3y)2-8y2;
(3)(x+2y-3)(x-2y+3);
(4)$\frac{1-{x}^{2}}{{x}^{2}+4x+4}$÷(x+1)2•$\frac{{x}^{2}+3x+2}{x-1}$.
分析 (1)原式利用幂的乘方与积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;
(2)原式利用完全平方公式展开,合并即可得到结果;
(3)原式利用平方差公式化简,再利用完全平方公式展开即可;
(4)原式利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=a2b4•(-a9b3)÷(-5ab)=$\frac{1}{5}$a10b6;
(2)原式=4x2-12xy+9y2-8y2=4x2-12xy+y2;
(3)原式=x2-(2y-3)2=x2-4y2+12y-9;
(4)原式=-$\frac{(x+1)(x-1)}{(x+2)^{2}}$•$\frac{1}{(x+1)^{2}}$•$\frac{(x+1)(x+2)}{x-1}$=-$\frac{1}{x+2}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
16.射击队对甲、乙两名运动员进行了六次测试,测试成绩如下表(单位:环):
分别计算甲、乙六次测试成绩的方差.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
17.计算$\frac{\sqrt{8}}{\sqrt{12}}÷\sqrt{\frac{45}{12}}×\sqrt{\frac{5}{8}}$的值是( )
| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{3\sqrt{3}}{4}$ |
18.如图,∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
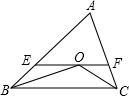 已知:如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于F.求∠BOC的度数.
已知:如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于F.求∠BOC的度数.