题目内容
19.已知关于x的方程x2+(2m-1)x+m2=0有实数根,(1)求m的取值范围;
(2)若方程的一个根为1,求m的值;
(3)设α、β是方程的两个实数根,是否存在实数m使得α2+β2-αβ=6成立?如果存在,请求出来,若不存在,请说明理由.
分析 (1)根据判别式的意义得到△=(2m-1)2-4m2≥0,然后解不等式即可;
(2)把x=1代入原方程可得到关于m的一元二次方程,然后解此一元二次方程即可;
(3)根据根与系数的关系得到α+β=-(2m-1),αβ=m2,利用α2+β2-αβ=6得到(α+β)2-3αβ=6,则(2m-1)2-3m2=6,然后解方程后利用(1)中m的范围确定m的值.
解答 解:(1)根据题意得△=(2m-1)2-4m2≥0,
解得m≤$\frac{1}{4}$;
(2)把x=1代入方程得1+2m-1+m2=0,
解得m1=0,m2=-2,
即m的值为0或-2;
(3)存在.
根据题意得α+β=-(2m-1),αβ=m2,
∵α2+β2-αβ=6,
∴(α+β)2-3αβ=6,
即(2m-1)2-3m2=6,
整理得m2-4m-5=0,解得m1=5,m2=-1,
∵m≤$\frac{1}{4}$;
∴m的值为-1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,反过来也成立.也考查了根的判别式.

练习册系列答案
相关题目
11.计算(a+2b)2的结果是( )
| A. | a2+4b2 | B. | a2+2ab+2b2 | C. | a2+4ab+2b2 | D. | a2+4ab+4b2 |
9. 如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )
如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )
 如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )
如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )| A. | DE=2 | |
| B. | △ADE的面积与△ABC的面积之比为1:4 | |
| C. | △ADE∽△ABC | |
| D. | △DEC的周长与△ABC的周长之比为1:2 |
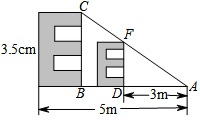 为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲同学设计的方案新颖,构思巧妙.甲生的方案:根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?
为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲同学设计的方案新颖,构思巧妙.甲生的方案:根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?