题目内容
13．若关于x的一元二次方程kx2-6x+9=0有两个相等的实数根，则该方程的根为（ ）| A． | x1=x2=3 | B． | x1=x2=1 | C． | x1=x2=-1 | D． | x1=x2=-3 |
分析 根据二次项系数非负结合根的判别式△=0，即可求出k值，将其代入原方程中，解之即可得出结论．
解答 解：∵关于x的一元二次方程kx2-6x+9=0有两个相等的实数根，
∴$\left\{\begin{array}{l}{k≠0}\\{△=（-6）^{2}-36k=0}\end{array}\right.$，
解得：k=1，
∴原方程为x2-6x+9=（x-3）2=0，
解得：x1=x2=3．
故选A．
点评 本题考查了根的判别式，牢记“当△=0时，方程有两个相等的实数根”是解题的关键．
练习册系列答案
相关题目
1．
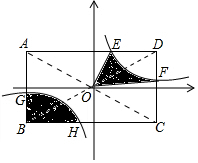如图，反比例函数y=$\frac{k}{x}$（k＞0）的图象与对角线交点在原点的矩形ABCD交于点E，F，G，H且E（1，3），AB：BC=$\frac{1}{2}$，图中阴影部分的面积为15．
如图，反比例函数y=$\frac{k}{x}$（k＞0）的图象与对角线交点在原点的矩形ABCD交于点E，F，G，H且E（1，3），AB：BC=$\frac{1}{2}$，图中阴影部分的面积为15． 
18．
如图，在长方体ABCD-EFGH中，与棱AD所在的直线既不相交也不平行的棱共有（ ）
如图，在长方体ABCD-EFGH中，与棱AD所在的直线既不相交也不平行的棱共有（ ）| A． | 1条 | B． | 2条 | C． | 3条 | D． | 4条 |
2．
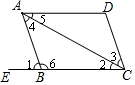如图，四边形ABCD，E是CB延长线上一点，下列推理正确的是（ ）
如图，四边形ABCD，E是CB延长线上一点，下列推理正确的是（ ）| A． | 如果∠1=∠2，那么AB∥CD | B． | 如果∠3=∠4，那么AD∥BC | ||
| C． | 如果AD∥BC，那么∠6+∠BAD=180° | D． | 如果∠6+∠BCD=180°，那么AD∥BC |