题目内容
计算:(1)
-|1-
|+cos45°-(-1)4
(2)解不等式
+1≥
x,并在数轴上表示其解集.
|
| 2 |
(2)解不等式
| 3-2x |
| 4 |
| 1 |
| 2 |
考点:实数的运算,在数轴上表示不等式的解集,解一元一次不等式,特殊角的三角函数值
专题:计算题
分析:(1)根据二次根式的化简、绝对值的意义和cos45°=
得到原式=
+(1-
)+
-1,然后合并即可;
(2)先利用不等式两边都乘以4得到3-2x+4≥2x,再移项、合并、系数化为1即可得到不等式的解集为,然后在数轴上表示解集.
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
(2)先利用不等式两边都乘以4得到3-2x+4≥2x,再移项、合并、系数化为1即可得到不等式的解集为,然后在数轴上表示解集.
解答:解:(1)原式=
+(1-
)+
-1
=0;
(2)去分母得3-2x+4≥2x,
移项、合并得-4x≥-7,
系数化为1得x≤
,
所以不等式的解集为x≤
,
在数轴上表示为: .
.
| ||
| 2 |
| 2 |
| ||
| 2 |
=0;
(2)去分母得3-2x+4≥2x,
移项、合并得-4x≥-7,
系数化为1得x≤
| 7 |
| 4 |
所以不等式的解集为x≤
| 7 |
| 4 |
在数轴上表示为:
 .
.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,最后进行加减运算.也考查了二次根式的化简、特殊角的三角函数值以及解一元一次不等式.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,桌面上放着两个物体,按下图所示的方式摆放在一起,其左视图是( )
如图,桌面上放着两个物体,按下图所示的方式摆放在一起,其左视图是( )A、 |
B、 |
C、 |
D、 |
 用15个
用15个 字形纸片和1个
字形纸片和1个 字纸片,能否盖满1个8×8方格棋盘.
字纸片,能否盖满1个8×8方格棋盘. 字形纸片和1个
字形纸片和1个 字纸片,能否盖满1个8×8方格棋盘.
字纸片,能否盖满1个8×8方格棋盘. 如图,已知双曲线
如图,已知双曲线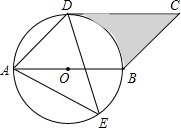 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°. 将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=
将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=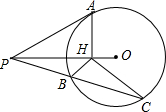 如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算
如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算