题目内容
13.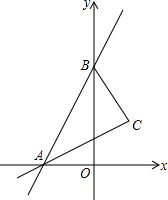 如图,直线y=7x+7交x轴于点A,交y轴于点B.
如图,直线y=7x+7交x轴于点A,交y轴于点B.(1)S△AOB;
(2)第一象限内是否存在点C,使△ABC为等腰直角三角形且∠ACB=90°?若存在,求出C点坐标;若不存在,请说明理由.
分析 (1)由直线解析式,分别令x与y为0求出y与x的值,确定出A与B坐标,进而求出OA与OB的长,即可求出三角形AOB面积;
(2)第一象限内存在点C,使△ABC为等腰直角三角形且∠ACB=90°,理由为:设C(x,y)(x>0,y>0),根据题意得BC2=AC2,BC2+AC2=AB2,列出关于x与y的方程组,求出方程组的解得到x与y的值,即可确定出C坐标.
解答 解:(1)对于直线y=7x+7,
令x=0,得到y=7;令y=0,得到x=-1,
∴A(-1,0),B(0,7),即OA=1,OB=7,
则S△AOB=$\frac{1}{2}$OA•OB=$\frac{7}{2}$;
(2)第一象限内存在点C,使△ABC为等腰直角三角形且∠ACB=90°,理由为:
设C(x,y)(x>0,y>0),
根据题意得:BC2=AC2,BC2+AC2=AB2,即$\left\{\begin{array}{l}{(-1-x)^{2}+{y}^{2}={x}^{2}+(y-7)^{2}}\\{(-1-x)^{2}+{y}^{2}+{x}^{2}+(y-7)^{2}={1}^{2}+{7}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
此时C(3,3).
点评 此题考查了一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,两点间的距离公式,以及等腰直角三角形的判定与性质,熟练掌握一次函数的性质是解本题的关键.

练习册系列答案
相关题目
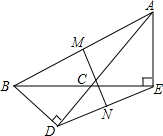 如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE.
如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE. 如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F. 已知:b是最小的正整数,且a、b满足(c-5)2+|a+b|=0,请回答问题:
已知:b是最小的正整数,且a、b满足(c-5)2+|a+b|=0,请回答问题: