题目内容
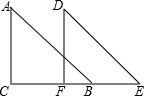 如图,在△ABC中,∠C=90°,AC=6,AB=10,平移△ABC得到△DEF,且点F在边BC上,DB=3
如图,在△ABC中,∠C=90°,AC=6,AB=10,平移△ABC得到△DEF,且点F在边BC上,DB=3| 5 |
考点:平移的性质,勾股定理
专题:
分析:先根据勾股定理求出BC的长,然后根据平移的性质可得:DF=AC=6,EF=BC=8,∠DFE=∠C=90°,连接BD,在Rt△DBF中,由勾股定理即可求出BF的值,然后根据CF=BC-BF,求出CF的值,最后由CE=CF+EF,即可求CE的长.
解答:解:连接BD,
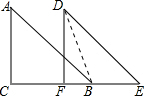
在△ABC中,∠C=90°,AC=6,AB=10,
由勾股定理得:
BC=
=8,
∵平移△ABC得到△DEF,
∴DF=AC=6,EF=BC=8,∠DFE=∠C=90°,
在Rt△DBF中,DB=3
,DF=6,由勾股定理得:
BF=
=3,
∵CF=BC-BF,
∴CF=8-3=5,
∵CE=CF+EF,
∴CE=5+8=13.

在△ABC中,∠C=90°,AC=6,AB=10,
由勾股定理得:
BC=
| AB2-AC2 |
∵平移△ABC得到△DEF,
∴DF=AC=6,EF=BC=8,∠DFE=∠C=90°,
在Rt△DBF中,DB=3
| 5 |
BF=
| BD2-DF2 |
∵CF=BC-BF,
∴CF=8-3=5,
∵CE=CF+EF,
∴CE=5+8=13.
点评:此题考查了平移的性质,根据平移的特点,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.关键是找出对应点,即可找出对应线段.注意结合图形解题的思想.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
下列说法正确的是( )
| A、某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,必有4次投中 | ||
| B、抽检1000件衬衣,其中不合格的衬衣有2件,由此估计任抽1件衬衣合格的概率为0.998 | ||
| C、任意抛掷一枚均匀的硬币两次,则第一次正面朝上且第二次背面朝上的概率为0.5 | ||
D、一局国际象棋比赛有胜、负与和局三种结果,你和任一对手下一局棋,出现和局的概率为
|
若x>y,则下列式子正确的是( )
| A、x-5>y+5 |
| B、5x>5y |
| C、-5x+3>-5y+3 |
| D、ax>ay |
 实数a在数轴上的位置如图所示,化简:
实数a在数轴上的位置如图所示,化简: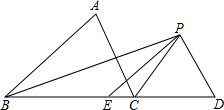 已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长.
已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长. 如图所示,OA,OB,OC都是⊙O的半径,∠ACB=45°,∠BOC=30°,求∠BAC与∠AOB的度数.
如图所示,OA,OB,OC都是⊙O的半径,∠ACB=45°,∠BOC=30°,求∠BAC与∠AOB的度数. 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若DP=6,则PE的长为( )
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若DP=6,则PE的长为( )