题目内容
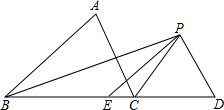 已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长.
已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长.考点:等腰三角形的判定与性质
专题:
分析:先由角平分线的定义可得∠ABP=∠CBP,∠ACP=∠DCP,再由平行线的性质得出∠ABP=∠BPE,∠ACP=∠CPD,得出∠CBP=∠BPE,∠DCP=∠CPD,证出BE=PE,PD=CD,即可求出△PED的周长.
解答:解:∵BP平分∠ABC,PD平分∠ACD,
∴∠ABP=∠CBP,∠ACP=∠DCP,
∵PD∥AC,PE∥AB,
∴∠ABP=∠BPE,∠ACP=∠CPD,
∴∠CBP=∠BPE,∠DCP=∠CPD,
∴BE=PE,PD=CD=6,
∴PE+ED+PD=BE+ED+PD=BD+CD=10+6=16.
∴∠ABP=∠CBP,∠ACP=∠DCP,
∵PD∥AC,PE∥AB,
∴∠ABP=∠BPE,∠ACP=∠CPD,
∴∠CBP=∠BPE,∠DCP=∠CPD,
∴BE=PE,PD=CD=6,
∴PE+ED+PD=BE+ED+PD=BD+CD=10+6=16.
点评:本题考查了等腰三角形的判定和角平分线的定义以及平行线的性质;由角平分线和平行线得出相等的角是证明三角形是等腰三角形的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列平面图形经过折叠后,能围成正方体的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
已知∠A=65°,则∠A的余角等于( )
| A、115° | B、55° |
| C、35° | D、25° |
已知二次函数y=-x2+bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
| A、b≥-2 | B、b≤-2 |
| C、b≥2 | D、b≤2 |
 如图,△ABC中,∠ACB=90°,∠A=30°,AC的中垂线交AC于E.交AB于D,则图中60°的角共有( )
如图,△ABC中,∠ACB=90°,∠A=30°,AC的中垂线交AC于E.交AB于D,则图中60°的角共有( )| A、6个 | B、5个 | C、4个 | D、3个 |
 已知如图,AC=BD,∠BAC=∠ABD,求证:AD=BC.
已知如图,AC=BD,∠BAC=∠ABD,求证:AD=BC. 有一工程勘测队为测量某个山坡上无法到达的A,B两处之间的距离,测得如下一些数据,如图,在山腰P处测得对面山脚A处的俯角(即∠FPA)为60°,测得对面山坡上B处的俯角(即∠FPB)为35°,已知∠BAC=30°,点P,E,A,B,C在同一平面上,点E,A,C在同一直线上,且PE⊥EC,AE=100米.
有一工程勘测队为测量某个山坡上无法到达的A,B两处之间的距离,测得如下一些数据,如图,在山腰P处测得对面山脚A处的俯角(即∠FPA)为60°,测得对面山坡上B处的俯角(即∠FPB)为35°,已知∠BAC=30°,点P,E,A,B,C在同一平面上,点E,A,C在同一直线上,且PE⊥EC,AE=100米.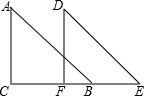 如图,在△ABC中,∠C=90°,AC=6,AB=10,平移△ABC得到△DEF,且点F在边BC上,DB=3
如图,在△ABC中,∠C=90°,AC=6,AB=10,平移△ABC得到△DEF,且点F在边BC上,DB=3