题目内容
20.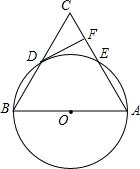 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求$\widehat{BD}$的长(结果保留π).
分析 (1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;
(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论.
解答 (1)证明:连接OD,如图所示.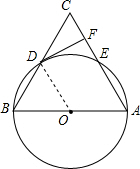
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°.
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC.
(2)解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°-∠CDF-∠ODF=60°.
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴$\widehat{BD}$的长=$\frac{nπR}{180}$=$\frac{60π×5}{180}$=$\frac{5}{3}$π.
点评 本题考查了切线的性质、弧长公式、平行线的性质、三角形中位线定理以及等边三角形的判断,解题的关键是:(1)求出∠CFD=∠ODF=90°;(2)找出△OBD是等边三角形.本题属于中档题,难度不大,解决该题型题目时,通过角的计算找出90°的角是关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8.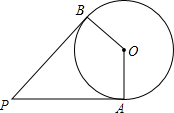 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )| A. | $\frac{2}{3}$π | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
15. 如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
 如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )| A. | x=2 | B. | x=0 | C. | x=-1 | D. | x=-3 |
5.不等式组$\left\{\begin{array}{l}{x-3<1}\\{3x+2≤4x}\end{array}\right.$的解集为( )
| A. | x≤2 | B. | x<4 | C. | 2≤x<4 | D. | x≥2 |
4.下面所给的图形中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.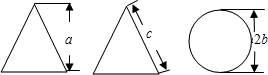 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )| A. | a>c | B. | b>c | C. | a2+4b2=c2 | D. | a2+b2=c2 |