题目内容
11.关于x的一元二次方程x2-4sinα•x+2=0有两个等根,则锐角α的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 先利用判别式的意义得到△=16sin2α-4×2=0,然后求出α的正弦值,再利用特殊角的三角函数值确定锐角α的度数.
解答 解:根据题意得△=16sin2α-4×2=0,
所以sinα=$\frac{\sqrt{2}}{2}$,
所以锐角α=45°.
故选B.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了特殊角的三角函数值.

练习册系列答案
相关题目
2.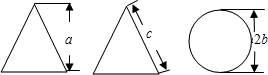 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )| A. | a>c | B. | b>c | C. | a2+4b2=c2 | D. | a2+b2=c2 |
6.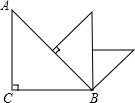 如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
 如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
3.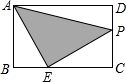 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上一点,且BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路程长x之间的函数关系用图象表示应为( )
如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上一点,且BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路程长x之间的函数关系用图象表示应为( )
 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上一点,且BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路程长x之间的函数关系用图象表示应为( )
如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上一点,且BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路程长x之间的函数关系用图象表示应为( )| A. |  | B. |  | C. | 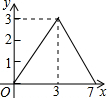 | D. | 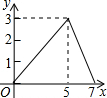 |
20.下列关于“-1”的说法中,错误的是( )
| A. | -1的相反数是1 | B. | -1是最小的负整数 | ||
| C. | -1的绝对值是1 | D. | -1是最大的负整数 |
1.一个圆锥的侧面展开图是半径为$\frac{1}{2}$的半圆,则该圆锥的底面半径是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
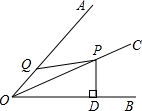
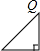
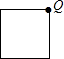
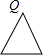
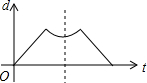 设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )
设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )