题目内容
11.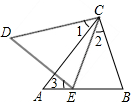 如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.
如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.
分析 由∠1=∠3、∠CFD=∠EFA知∠D=∠A,由∠1=∠2知∠DCE=∠ACB,由∠CEB=∠B知CE=CB,从而证△DCE≌△ACB得CD=CA.
解答 证明:如图,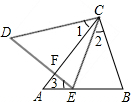
∵∠1=∠3,∠CFD=∠EFA,
∴180°-∠1-∠CFD=180°-∠3-∠EFA,即∠D=∠A,
∵∠1=∠2,
∴∠1+∠ACE=∠2+∠ACE,即∠DCE=∠ACB,
又∵∠CEB=∠B,
∴CE=CB,
在△DCE和△ACB中,
∵$\left\{\begin{array}{l}{∠D=∠A}\\{∠DCE=∠ACB}\\{CE=CB}\end{array}\right.$,
∴△DCE≌△ACB(AAS),
∴CD=CA.
点评 本题主要考查全等三角形的判定与性质、三角形的内角和定理、等角对等边,熟练掌握三角形的内角和定理、等角对等边得出角相等或边相等是证明三角形全等的关键.

练习册系列答案
相关题目
16.已知二次函数y=x2+8x+12与x轴的交点为A,C(点A在点C的左侧),与y轴的交点为B,顶点部分为D,若点P(x,y)是四边形ABCD边上的点,则3x-y的最大值为( )
| A. | -6 | B. | -8 | C. | -12 | D. | -18 |
3.在平面直角坐标系中,若直线y=-x+a与直线y=2x+b(a,b为常数)的交点M(3,-1),则关于x的不等式-x+a≥2x+b的解集为( )
| A. | x≤3 | B. | x≥3 | C. | x≤-1 | D. | x≥-1 |
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与X轴交于点A、B两点B处的坐标为(3,0),与y轴交于c(0,-3),点P是直线BC下方抛物线上的动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与X轴交于点A、B两点B处的坐标为(3,0),与y轴交于c(0,-3),点P是直线BC下方抛物线上的动点.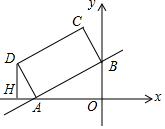 如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.
如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.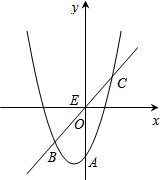 顶点为(-$\frac{1}{2}$,-$\frac{17}{4}$)的抛物线与y轴交于点A(0,-4),E(0,b)(b>-4)为y轴上一动点,过点E的直线y=x+b与抛物线交于B、C两点.
顶点为(-$\frac{1}{2}$,-$\frac{17}{4}$)的抛物线与y轴交于点A(0,-4),E(0,b)(b>-4)为y轴上一动点,过点E的直线y=x+b与抛物线交于B、C两点. 作图题,在铁路旁边有一城镇,现在要建立一个火车站,为了使城镇的人乘火车方便(距离火车站最近),应怎样确定火车站的位置呢?请你作图说明,并解释其依据,其依据是:垂线段最短.
作图题,在铁路旁边有一城镇,现在要建立一个火车站,为了使城镇的人乘火车方便(距离火车站最近),应怎样确定火车站的位置呢?请你作图说明,并解释其依据,其依据是:垂线段最短.