题目内容
20.在平面直角坐标系中,二次函数图象交x轴于(-5,0)、(1,0)两点,将此二次函数图象向右平移m个单位,再向下平移n个单位后,发现新的二次函数图象与x轴交于(-1,0)、(3,0)两点,则m的值为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 根据平移前后抛物线对称轴的变化即可得出答案.
解答 解:∵二次函数图象交x轴于(-5,0)、(1,0)两点,
∴原二次函数的对称轴为$\frac{-5+1}{2}$=-2,
∵新的二次函数图象与x轴交于(-1,0)、(3,0)两点,
∴原二次函数的对称轴为x=$\frac{-1+3}{2}$=1,
∴原抛物线向右平移了3个单位,即m=3,
故选:A.
点评 本题主要考查二次函数图象与x轴的交点及抛物线的平移,根据题意得出平移前后抛物线对称轴的变化是解题的关键.

练习册系列答案
相关题目
8.下列计算正确的是( )
| A. | 5a-2a=3 | B. | (2a2)3=6a6 | C. | 3a•(-2a)4=48a5 | D. | a3+2a=2a2 |
15.已知正比例函数y=(m-1)x+m2-m-2的图象经过二、四象限,那么m的值是( )
| A. | m=1 | B. | m=-1 | C. | m=2 | D. | m=-2 |
 将一副三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是72cm2.
将一副三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是72cm2.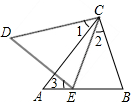 如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.
如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.