题目内容
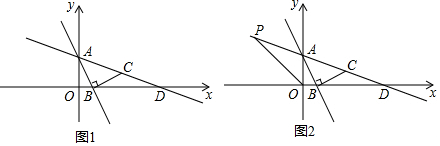
16.已知二次函数y=x2+8x+12与x轴的交点为A,C(点A在点C的左侧),与y轴的交点为B,顶点部分为D,若点P(x,y)是四边形ABCD边上的点,则3x-y的最大值为( )| A. | -6 | B. | -8 | C. | -12 | D. | -18 |
分析 令y=0,求得与x轴的交点坐标,令x=0,求得与y轴的交点坐标,根据顶点式解析式得顶点坐标,设z=3x-y,则y=3x-z.如图由函数y=3x-z的图象可知,欲求z的最大值,可以转化为求直线y=3x-z与y轴交点的纵坐标的最小值即可,
解答 解:令y=0,则x2+8x+12=0,
解得:x1=-2,x2=-6,
∵点A在点C的左侧,
∴A(-6,0)、C(-2,0),
令x=0,则y=12,
与y轴交点坐标为B(0,12),
∵y=(x+4)2-4
∴顶点坐标D为(-4,-4).
设z=3x-y,则y=3x-z.
如图由函数y=3x-z的图象可知,欲求z的最大值,可以转化为求直线y=3x-z与y轴交点的纵坐标的最小值即可,
由图象可知当直线经过点C时-z的值最小,z的值最大,
把(-2,0)代入y=3x-z,得到z=-6,
∴z的最大值为-6.
故选A.
点评 本题主要考查了抛物线与坐标轴的交点、顶点坐标、一次函数的应用等知识,解题的关键是学会用转化思想、数形结合思想解决问题.

练习册系列答案
相关题目
11.如图,下面表格给出的是国外四个城市与北京的时差(带“+”表示同一时刻比北京时间早的时数),如果现在悉尼时间是下午6时,则伦敦时间是上午8点.
| 城市 | 纽约 | 悉尼 | 伦敦 | 罗马 |
| 时差/h | -13 | +2 | -8 | -7 |
1.对于正比例函数y=kx(k≠0),当自变量x的值减小2时,函数y的值减小-6,则k的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
8.下列计算正确的是( )
| A. | 5a-2a=3 | B. | (2a2)3=6a6 | C. | 3a•(-2a)4=48a5 | D. | a3+2a=2a2 |
6.函数y=-x2+2x-3,顶点坐标为( )
| A. | (-1,-2) | B. | (-1,-3) | C. | (1,-3) | D. | (1,-2) |
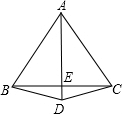 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB=6cm.
如图,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB=6cm.
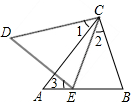 如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.
如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.