题目内容
2. 如图,Rt△ABC中,∠C=90°,AC=5,BC=2,将AB所在的直线绕点A旋转45°,交直线BC于D,则DB的长度为$\frac{29}{7}$或$\frac{29}{3}$.
如图,Rt△ABC中,∠C=90°,AC=5,BC=2,将AB所在的直线绕点A旋转45°,交直线BC于D,则DB的长度为$\frac{29}{7}$或$\frac{29}{3}$.
分析 ①如图1,由旋转的性质得到∠DAE=45°,根据勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{29}$,过D作DE⊥AB于E,设AE=DE=x,得到BE=$\sqrt{29}$-x,根据相似三角形的性质得到$\frac{DE}{AC}=\frac{BE}{BC}$,即$\frac{x}{5}=\frac{\sqrt{29}-x}{2}$,求得DE=$\frac{5\sqrt{29}}{7}$,BE=$\frac{2\sqrt{29}}{7}$,根据勾股定理得到结论;
②如图2,由旋转的性质得到∠DAE=45°根据勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{29}$,过D作DE⊥AB于E,设AE=DE=x,得到BE=x-$\sqrt{29}$,根据相似三角形的性质得到$\frac{BE}{BC}=\frac{DE}{AC}$,即$\frac{x-\sqrt{29}}{2}=\frac{x}{5}$,求得DE=$\frac{5\sqrt{29}}{3}$,BE=$\frac{2\sqrt{29}}{3}$,根据勾股定理即可得到结论.
解答 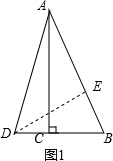 解:①如图1,将AB所在的直线绕点A顺时针旋转45°,
解:①如图1,将AB所在的直线绕点A顺时针旋转45°,
则∠DAE=45°,
∵∠ACB=90°,AC=5,BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{29}$,
过D作DE⊥AB于E,
∴AE=DE,
设AE=DE=x,
∴BE=$\sqrt{29}$-x,
∵∠ACB=∠DEB=90°,∠B=∠B,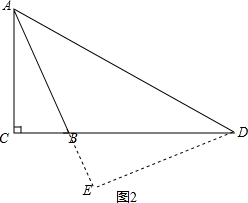
∴△DEB∽△ACB,
∴$\frac{DE}{AC}=\frac{BE}{BC}$,即$\frac{x}{5}=\frac{\sqrt{29}-x}{2}$,
∴x=$\frac{5\sqrt{29}}{7}$,
∴DE=$\frac{5\sqrt{29}}{7}$,BE=$\frac{2\sqrt{29}}{7}$,
∴BD=$\sqrt{D{E}^{2}+B{E}^{2}}$=$\frac{29}{7}$;
②如图2,将AB所在的直线绕点A逆时针旋转45°,
则∠DAE=45°,
∵∠ACB=90°,AC=5,BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{29}$,
过D作DE⊥AB于E,
∴AE=DE,
设AE=DE=x,
∴BE=x-$\sqrt{29}$,
∵∠ACB=∠DEB=90°,∠ABC=∠DBE,
∴△DEB∽△ACB,
∴$\frac{BE}{BC}=\frac{DE}{AC}$,即$\frac{x-\sqrt{29}}{2}=\frac{x}{5}$,
∴x=$\frac{5\sqrt{29}}{3}$,
∴DE=$\frac{5\sqrt{29}}{3}$,BE=$\frac{2\sqrt{29}}{3}$,
∴BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\frac{29}{3}$.
综上所述:DB的长度为$\frac{29}{7}$或$\frac{29}{3}$,
故答案为:$\frac{29}{7}$或$\frac{29}{3}$.
点评 本题主要考查了旋转的性质,等腰直角三角形,相似三角形的判定和性质,熟练掌握旋转的性质是解决问题的关键.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -$\frac{1}{2}$ |
 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )| A. | (4032,0) | B. | (4032,2$\sqrt{3}$) | C. | (4031,$\sqrt{3}$) | D. | (4033,$\sqrt{3}$) |
 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{4}{15}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
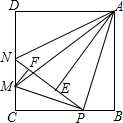 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①②⑤(写出所有正确结论的序号)
如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①②⑤(写出所有正确结论的序号)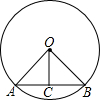 如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为$\sqrt{13}$.
如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为$\sqrt{13}$. 如图,数轴上P、Q、S、T四点对应的整数分别是p、q、s、t,且有p+q+s+t=-2,那么,原点应是点( )
如图,数轴上P、Q、S、T四点对应的整数分别是p、q、s、t,且有p+q+s+t=-2,那么,原点应是点( )