题目内容
14. 如图,数轴上P、Q、S、T四点对应的整数分别是p、q、s、t,且有p+q+s+t=-2,那么,原点应是点( )
如图,数轴上P、Q、S、T四点对应的整数分别是p、q、s、t,且有p+q+s+t=-2,那么,原点应是点( )| A. | P | B. | Q | C. | S | D. | T |
分析 根据数轴可以分别假设原点在P、Q、S、T,然后分别求出p+q+s+t的值,从而可以判断原点在什么位置,本题得以解决.
解答 解:由数轴可得,
若原点在P点,则p+q+s+t=10,
若原点在Q点,则p+q+s+t=6,
若原点在S点,则p+q+s+t=-2,
若原点在T点,则p+q+s+t=-14,
∵数轴上P、Q、S、T四点对应的整数分别是p、q、s、t,且有p+q+s+t=-2,
∴原点应是点S,
故选C.
点评 本题考查数轴,解题的关键是明确数轴的特点,利用数形结合的思想解答问题.

练习册系列答案
相关题目
17.对于一组数据-1,-1,4,2,下列结论不正确的是( )
| A. | 平均数是1 | B. | 众数是-1 | C. | 中位数是0.5 | D. | 方差是3.5 |
9.将一张大小为10cm×10cm的正方形纸片,依下图所示方式折叠并剪裁后再展开,其中折线(虚线)正好过三角形两边的中点,则展开后内部的正方形(无阴影部分)面积等于( )


| A. | 25cm2 | B. | 50cm2 | C. | 75cm2 | D. | 40cm |
6.以下列各组线段为边,能组成三角形的是( )
| A. | 1cm,2cm,4cm | B. | 4cm,6cm,8cm | C. | 5cm,6cm,12cm | D. | 2cm,3cm,5cm |
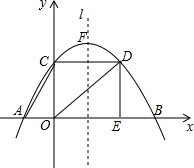 如图,已知抛物线y=ax2+bx+c经过点A(-3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
如图,已知抛物线y=ax2+bx+c经过点A(-3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点. 如图,Rt△ABC中,∠C=90°,AC=5,BC=2,将AB所在的直线绕点A旋转45°,交直线BC于D,则DB的长度为$\frac{29}{7}$或$\frac{29}{3}$.
如图,Rt△ABC中,∠C=90°,AC=5,BC=2,将AB所在的直线绕点A旋转45°,交直线BC于D,则DB的长度为$\frac{29}{7}$或$\frac{29}{3}$. 如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.
如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.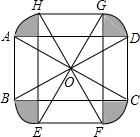 如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$.
如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$.