题目内容
7.化简(1)$\sqrt{1-2x+x^2}$+$\sqrt{x^2-8x+16}$.(1≤x<4)
(2)($\sqrt{2-x}$)2-$\sqrt{x^2-6x+9}$.
分析 (1)根据二次根式的性质和合并同类项的法则进行化简即可;
(2)根据二次根式有意义的条件、二次根式的性质和合并同类项的法则进行化简即可.
解答 解:(1)∵1≤x<4,
∴x-1≥0,x-4<0,
∴$\sqrt{1-2x+x^2}$+$\sqrt{x^2-8x+16}$
=$\sqrt{(1-x)^{2}}$+$\sqrt{(x-4)^{2}}$
=|1-x|+|x-4|
=x-1+4-x
=3;
(2)由题意得,2-x≥0,则3-x>0,
则($\sqrt{2-x}$)2-$\sqrt{x^2-6x+9}$
=2-x-(3-x)
=2-x-3+x
=-1.
点评 本题考查的是二次根式的化简,掌握二次根式的性质:$\sqrt{{a}^{2}}$=|a|是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.已知一组数据75,80,80,85,90,则它的众数和中位数分别为( )
| A. | 75,80 | B. | 80,85 | C. | 80,90 | D. | 80,80 |
12.已知∠1=37°36′,∠2=37.36°,则∠1与∠2的大小关系为( )
| A. | ∠1<∠2 | B. | ∠1=∠2 | C. | ∠1>∠2 | D. | 无法比较 |
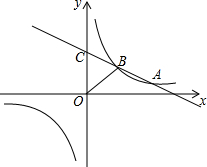 如图,一次函数y=kx+b(k<0)与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
如图,一次函数y=kx+b(k<0)与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) 如图,Rt△ABC中,∠C=90°,AC=5,BC=2,将AB所在的直线绕点A旋转45°,交直线BC于D,则DB的长度为$\frac{29}{7}$或$\frac{29}{3}$.
如图,Rt△ABC中,∠C=90°,AC=5,BC=2,将AB所在的直线绕点A旋转45°,交直线BC于D,则DB的长度为$\frac{29}{7}$或$\frac{29}{3}$. 如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.
如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.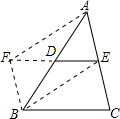 完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.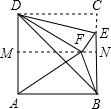 将-张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上-点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD,则得下列结论:
将-张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上-点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD,则得下列结论: