题目内容
 如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于点F,若BE=1,AB=3,则PF的长为
如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于点F,若BE=1,AB=3,则PF的长为考点:正方形的性质,全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:连接AP.根据四边形ABCD是正方形的性质得出AB=BC,∠ABP=∠CBP=45°,证△ABP≌△CBP,推出PA=PC,∠3=∠4,求出∠3=∠5,得出△APE是等腰直角三角形,求出AE,即可求出PE.
解答:解:连接AP.
∵四边形ABCD是正方形,
∴AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠3=∠4,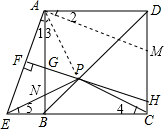
∵PE=PC,
∴PA=PE,
∵PE=PC,
∴∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴∠3+∠ANP=∠5+∠ENB=90°,
∴AP⊥PE,即△APE是等腰直角三角形,
∵BE=1,AB=3,
∴AE=
=
,
∴PE=
=
=
.
∴PF=
PE=
.
故答案是:
.
∵四边形ABCD是正方形,
∴AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴PA=PC,∠3=∠4,

∵PE=PC,
∴PA=PE,
∵PE=PC,
∴∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴∠3+∠ANP=∠5+∠ENB=90°,
∴AP⊥PE,即△APE是等腰直角三角形,
∵BE=1,AB=3,
∴AE=
| 12+32 |
| 10 |
∴PE=
| AE | ||
|
| ||
|
| 5 |
∴PF=
| ||
| 2 |
| ||
| 2 |
故答案是:
| ||
| 2 |
点评:本题考查了正方形的性质和判定,勾股定理,等腰三角形性质,等腰直角三角形性质,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
下列实数中,无理数是( )
| A、3.14 | |||
| B、-234.10101010…(相邻两个1之间有1个0) | |||
C、
| |||
| D、0.12345678910111213…(小数部分由相继的正整数组成) |
 如图所示,已知△ABC中,BD:DC=3:2,AF:FD=2:1,求AE:EC.
如图所示,已知△ABC中,BD:DC=3:2,AF:FD=2:1,求AE:EC.