题目内容
如果三角形的三边a、b、c满足(a-c)2+|c-b|=0,那么这个三角形是 三角形.
考点:等边三角形的判定,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:由题意得:a-c=0,c-b=0,得到a=b=c,即可解决问题.
解答:解:∵(a-c)2+|c-b|=0,且(a-c)2≥0,|c-b|≥0,
∴a-c=0,c-b=0,
∴a=b=c,即该三角形为等边三角形.
故答案为:等边.
∴a-c=0,c-b=0,
∴a=b=c,即该三角形为等边三角形.
故答案为:等边.
点评:该题主要考查了非负数的性质、等边三角形的判定及其应用问题;应牢固掌握.

练习册系列答案
相关题目
抛物线y=(x+1)2-3的对称轴是( )
| A、y轴 | B、直线x=-1 |
| C、直线x=1 | D、直线x=-3 |
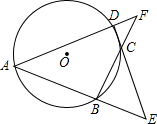 如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )
如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )| A、30° | B、40° |
| C、57° | D、70° |
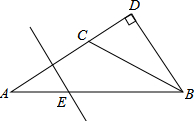 如图,△ABD中∠D=90°,C为AD上一点,且AC=BC=2CD,AC的垂直平分线交AB于E,求
如图,△ABD中∠D=90°,C为AD上一点,且AC=BC=2CD,AC的垂直平分线交AB于E,求 如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于点F,若BE=1,AB=3,则PF的长为
如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于点F,若BE=1,AB=3,则PF的长为