题目内容
12.数学家发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:$\sqrt{{a^2}+{b^2}+1}$.例如把(3,-2)放入其中,就会得到$\sqrt{{3^2}+{{(-2)}^2}+1}=\sqrt{14}$.现将实数对(-2,1)放入其中得到实数m,再将实数对(m,-2)放入其中后,得到的实数是$\sqrt{11}$.分析 根据题中的新定义确定出m的值,即可确定出所求实数.
解答 解:根据题中的新定义得:m=$\sqrt{(-2)^{2}+{1}^{2}+1}$=$\sqrt{6}$,
则将实数对(m,-2)放入其中后,得到的实数是$\sqrt{(\sqrt{6})^{2}+(-2)^{2}+1}$=$\sqrt{11}$,
故答案为:$\sqrt{11}$
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如果一个三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“动感三角形”.下列各组数据中,能作为一个动感三角形三边长的一组是( )
| A. | 1,2,3 | B. | 1,1,$\sqrt{2}$ | C. | 1,1,$\sqrt{3}$ | D. | 1,2,$\sqrt{3}$ |
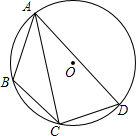 在⊙O的内接四边形ABCD中,AB=6,AD=10,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{16}{3}$$\sqrt{3}$.
在⊙O的内接四边形ABCD中,AB=6,AD=10,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{16}{3}$$\sqrt{3}$. 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.点Q在直线AB上,点P在x轴上,且∠OQP=90°.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.点Q在直线AB上,点P在x轴上,且∠OQP=90°.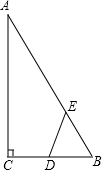 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为2秒或3.5秒或4.5秒.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为2秒或3.5秒或4.5秒.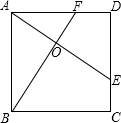 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..