题目内容
13. 如图,已知正六边形ABCDEF内接于⊙O,且边长为4.
如图,已知正六边形ABCDEF内接于⊙O,且边长为4.(1)求该正六边形的半径、边心距和中心角;
(2)求该正六边形的外接圆的周长和面积.
分析 (1)作辅助线;求出中心角,证明△OAB为等边三角形;运用边角关系求出OA的长度,进而求出边心距OM;
(2)由圆的周长和面积公式即可得出答案.
解答 解:如图,AB为⊙0的内接正六边形的一边,连接OA、OB;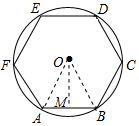
过点O作OM⊥AB于点M;
∵六边形ABCDEF为正六边形,
∴OA=OB,∠AOB=$\frac{1}{6}$=60°;
∴△OAB为等边三角形,
∴OA=AB=4;
∵OM⊥AB,
∴∠AOM=∠BOM=30°,AM=$\frac{1}{2}$AB=2,
∴OM=$\sqrt{3}$AM=2$\sqrt{3}$;
(2)正六边形的外接圆的周长=2π×OA=8π;
外接圆的面积=π×42=16π.
点评 本题考查的是正六边形的性质,解答此题的关键是熟知正六边形的边长等于半径.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
4.计算a•a5-(2a3)2的结果为( )
| A. | a6-2a5 | B. | -a6 | C. | a6-4a5 | D. | -3a6 |
5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
给出下列结论:
①m=-1
②当x>1时,y的值随x值的增大而减小
③3是方程ax2+(b-1)x+c=0的一个根
④若ax2+(b-1)x+c<0,则-1<x<3,其中正确的是( )
| X | -1 | 0 | 1 | 3 | 4 |
| y | -1 | 3 | 5 | 3 | m |
①m=-1
②当x>1时,y的值随x值的增大而减小
③3是方程ax2+(b-1)x+c=0的一个根
④若ax2+(b-1)x+c<0,则-1<x<3,其中正确的是( )
| A. | ①③ | B. | ③④ | C. | ①③④ | D. | ①②④ |
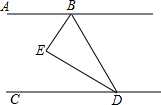 如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直线CD上一动点,(不与点D重合),BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直线CD上一动点,(不与点D重合),BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由. (1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法.
(1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法. 如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有6个.
如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有6个.