题目内容
13.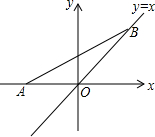 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
分析 过点A作AD⊥OB于点D,过点D作OE⊥x轴于点E,先根据垂线段最短得出当点B与点D重合时线段AB最短,再根据直线OB的解析式为y=x得出△AOD是等腰直角三角形,故OE=$\frac{1}{2}$OA=$\frac{\sqrt{2}}{2}$,由此可得出结论.
解答 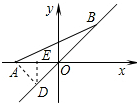 解:过点A作AD⊥OB于点D,过点D作OE⊥x轴于点E,
解:过点A作AD⊥OB于点D,过点D作OE⊥x轴于点E,
∵垂线段最短,
∴当点B与点D重合时线段AB最短.
∵直线OB的解析式为y=x,
∴△AOD是等腰直角三角形,
∴OE=$\frac{1}{2}$OA=$\frac{\sqrt{2}}{2}$,
∴D(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),
∴点B的坐标(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
8.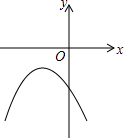 二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
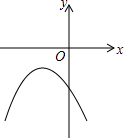 二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )| A. | a>0 | B. | b>0 | C. | c>0 | D. | abc<0 |
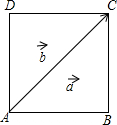 如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.
如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.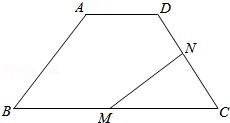 如图,在梯形ABCD中,AD∥BC,AD=3,CD=5,BC=10,梯形的高为4,动点M从点B出发沿线段BC以每秒2个单位长度向终点C运动;动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒
如图,在梯形ABCD中,AD∥BC,AD=3,CD=5,BC=10,梯形的高为4,动点M从点B出发沿线段BC以每秒2个单位长度向终点C运动;动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒