题目内容
4.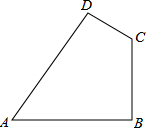 如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.
如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.
分析 连接AC,然后根据勾股定理求出AC的值,然后根据勾股定理的逆定理判断△ADC为Rt△,然后根据四边形的内角和定理即可得到∠A与∠C关系.
解答 证明:猜想∠A与∠C关系为:∠A+∠C=180°.
连结AC,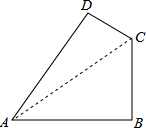
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=25cm,
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=180°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°.
点评 此题考查了勾股定理及勾股定理的逆定理,解题的关键是:根据勾股定理的逆定理判断△ADC是直角三角形.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
7.点P1(2,y1),P2(4,y2)是一次函数y=(m-2)x+m图象上的两个点,若y1<y2,则m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m>2 | D. | m<2 |
8.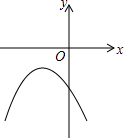 二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
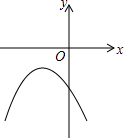 二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )| A. | a>0 | B. | b>0 | C. | c>0 | D. | abc<0 |

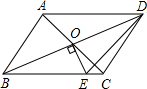 如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为12cm.
如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为12cm.