题目内容
18．把下列各式进行因式分解：（1）（x2+4）2-（2x+3）2
（2）4a2b2-（a2+b2）2．
分析 （1）原式利用平方差公式分解即可；
（2）原式利用平方差公式及完全平方公式分解即可．
解答 解：（1）原式=（x2+4+2x+3）（x2+4-2x-3）=（x2+2x+7）（x-1）2；
（2）原式=（2ab+a2+b2）（2ab-a2-b2）=-（a+b）2（a-b）2．
点评 此题考查了因式分解-运用公式法，熟练掌握完全平方公式及平方差公式是解本题的关键．
练习册系列答案
相关题目
9．
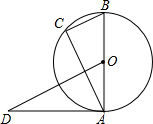如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为（ ）
如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
如图，过?ABCD的各顶点分别作对角线的垂线AE、BF、CG、DH．垂足分别为E、F、G、H．求证：四边形EFGH是平行四边形．
8．如果$\frac{1}{3}$xa+2y3与-3x3y2b-a是同类项，那么a，b的值分别是（ ）
| A． | $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=0}\\{b=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ |