题目内容
8.化简:(1)(a+b)2-(a+b)(a-b)+2a(a-b)
(2)($\frac{{x}^{2}-2x}{x-1}+2-x$)$÷\frac{{x}^{2}-4x+4}{1-x}$.
分析 (1)原式利用完全平方公式,平方差公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=a2+2ab+b2-a2+b2+2a2-2ab
=2a2+2b2;
(2)原式=$\frac{{x}^{2}-2x+(2-x)(x-1)}{x-1}$•$\frac{1-x}{(x-2)^{2}}$
=-$\frac{x-2}{x-1}$•$\frac{x-1}{(x-2)^{2}}$
=-$\frac{1}{x-2}$.
点评 此题考查了分式的混合运算,以及整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.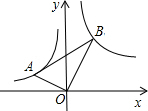 如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )
如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )
 如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )
如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )| A. | 4 | B. | 6 | C. | -8 | D. | 8 |
20.下列计算中,错误的是( )
| A. | 3a-2a=a | B. | -2a(3a-1)=-6a2-1 | ||
| C. | -8a2÷2a=-4a | D. | (a+3b)2=a2+6ab+9b2 |
17.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间平均距离,即1.4960亿千米,用科学记数法表示1个天文单位应是( )
| A. | 1.4960×107千米 | B. | 14.960×107千米 | C. | 1.4960×108千米 | D. | 0.14960×109千米 |
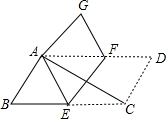 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,