题目内容
9.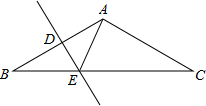 如图所示,底边BC为2$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
如图所示,底边BC为2$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )| A. | 2+2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 4 | D. | 3$\sqrt{3}$ |
分析 过A作AF⊥BC于F,根据等腰三角形的性质得到∠B=∠C=30°,得到AB=AC=2,根据线段垂直平分线的性质得到BE=AE,即可得到结论.
解答  解:过A作AF⊥BC于F,
解:过A作AF⊥BC于F,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,BF=CF=$\sqrt{3}$,
∵$\frac{BF}{AB}$=$\frac{\sqrt{3}}{2}$,
∴AB=AC=2,
∵DE垂直平分AB,
∴BE=AE,
∴AE+CE=BC=2$\sqrt{3}$,
∴△ACE的周长=AC+AE+CE=AC+BC=2+2$\sqrt{3}$,
故选:A.
点评 本题考查了线段垂直平分线性质,三角形的内角和定理,等腰三角形的性质,含30度角的直角三角形性质等知识点,主要考查运用性质进行推理的能力.

练习册系列答案
相关题目
20.四个命题:①三角形的一条中线能将三角形分成面积相等的两部分;②有两边和其中一边的对角分别相等的两个三角形全等;③点P(1,2)关于原点的对称点坐标为(-1,-2);④对角线互相垂直的四边形是菱形,其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
4.将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
| A. | y=(x+1)2-13 | B. | y=(x-5)2-3 | C. | y=(x-5)2-13 | D. | y=(x+1)2-3 |
14. 如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2等于( )
如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2等于( )
 如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2等于( )
如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2等于( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
1.下列运算正确的是( )
| A. | 3a+2a=5a2 | B. | a6÷a2=a3 | C. | (-3a3)2=9a6 | D. | (a+2)2=a2+4 |
18. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )| A. | 140米 | B. | 150米 | C. | 160米 | D. | 240米 |