题目内容
5.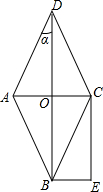 如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.(1)求证:四边形OBEC是矩形;
(2)若菱形ABCD的周长是4$\sqrt{10}$,tanα=$\frac{1}{2}$,求四边形OBEC的面积.
分析 (1)利用菱形的对角线互相垂直结合平行线的性质得出∠BOC=∠OCE=∠OBE=90°,进而求出即可;
(2)利用菱形的性质结合勾股定理得出CO,BO的长,进而求出四边形OBEC的面积.
解答 (1)证明:∵菱形ABCD的对角线AC与BD相交于点O,
∴AC⊥BD,
∵BE∥AC,CE∥BD,
∴∠BOC=∠OCE=∠OBE=90°,
∴四边形OBEC是矩形;
(2)解:∵菱形ABCD的周长是4$\sqrt{10}$,
∴AB=BC=AD=DC=$\sqrt{10}$,
∵tanα=$\frac{1}{2}$,
∴设CO=x,则BO=2x,
∴x2+(2x)2=($\sqrt{10}$)2,
解得:x=$\sqrt{2}$,
∴四边形OBEC的面积为:$\sqrt{2}$×2$\sqrt{2}$=4.
点评 此题主要考查了菱形的性质和判定以及勾股定理等知识,熟练利用菱形的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.不等式组$\left\{\begin{array}{l}{x-3≥0}\\{\frac{1}{2}(x+3)≤1}\end{array}\right.$的解集在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. | 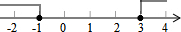 |
14.下列说法正确的是( )
| A. | 面积相等的两个三角形全等 | |
| B. | 矩形的四条边一定相等 | |
| C. | 一个图形和它旋转后所得图形的对应线段相等 | |
| D. | 随机投掷一枚质地均匀的硬币,落地后一定是正面朝上 |
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).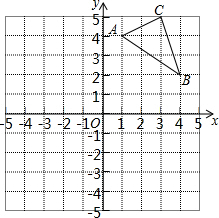 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).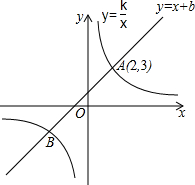 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).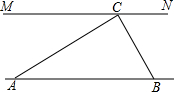 为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)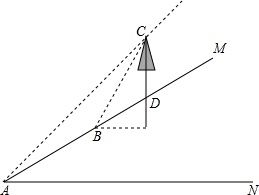 张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732)
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732) 如图在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在CE的中点A′处,则折痕DE的长为( )
如图在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在CE的中点A′处,则折痕DE的长为( )