题目内容
17.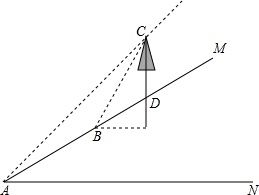 张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732)
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732)
分析 过B作BE⊥CD交CD延长线于E,由∠CAN=45°,∠MAN=30°,得到∠CAB=15°,由∠CBD=60°,∠DBE=30°,得到∠CBD=30°于是有∠CAB=∠ACB=15°所以AB=BC=20,解Rt△BCE,可求得CE,解Rt△DBE可求得DE,CE-DE即得到树高CD.
解答  解:如图,过B作BE⊥CD交CD延长线于E,
解:如图,过B作BE⊥CD交CD延长线于E,
∵∠CAN=45°,∠MAN=30°,
∴∠CAB=15°
∵∠CBE=60°,∠DBE=30°,
∴∠CBD=30°,
∵∠CBD=∠CAB+∠ACB,
∴∠CAB=∠ACB=15°,
∴AB=BC=20,
在Rt△BCE中,∠CBE=60°,BC=20,
∴CE=BCsin∠CBE=20×$\frac{\sqrt{3}}{2}=10\sqrt{3}$BE=BCcos∠CBE=20×0.5=10,
在Rt△DBE中,∠DBE=30°,BE=10,
∴DE=BEtan∠DBE=10×$\frac{\sqrt{3}}{3}=\frac{10\sqrt{3}}{3}$,
∴CD=CE-DE=$10\sqrt{3}-\frac{10\sqrt{3}}{3}=\frac{20\sqrt{3}}{3}$≈11.5,
答:这棵大树CD的高度大约为11.5米.
点评 本题主要考查了等腰三角形的判定与性质,解直角三角形,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | 22=4 | B. | 20=0 | C. | 2-1=-2 | D. | $\sqrt{4}$=±2 |
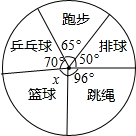 如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.
如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.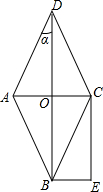 如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.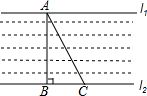 如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)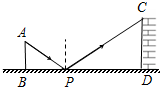 如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )
如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )