题目内容
16. 如图在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在CE的中点A′处,则折痕DE的长为( )
如图在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在CE的中点A′处,则折痕DE的长为( )| A. | 1 | B. | 6 | C. | 4 | D. | 2 |
分析 先由图形翻折变换的性质得出AE=A′E,再根据A′为CE的中点可知AE=A′E=$\frac{1}{2}$CE,故AE=$\frac{1}{3}$AC,$\frac{AE}{CE}$=$\frac{1}{3}$,再由∠C=90°,DE⊥AC可知DE∥BC,故可得出△ADE∽△ABC,由相似三角形的性质可知$\frac{DE}{BC}$=$\frac{AE}{BC}$=$\frac{1}{3}$,故可得出结论.
解答 解:∵△A′DE△ADE翻折而成,
∴AE=A′E,
∵A′为CE的中点,
∴AE=A′E=$\frac{1}{2}$CE,
∴AE=$\frac{1}{3}$AC,$\frac{AE}{CE}$=$\frac{1}{3}$,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AE}{BC}$=$\frac{1}{3}$,
∴$\frac{DE}{6}=\frac{1}{3}$,
解得DE=2.
故选:D.
点评 本题考查的是图形的翻折变换及相似三角形的判定与性质,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
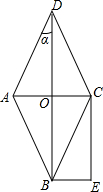 如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.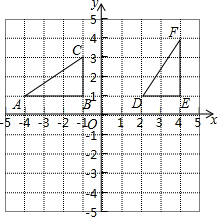 如图,△ABC和△DEF在直角坐标系中的位置如图所示.
如图,△ABC和△DEF在直角坐标系中的位置如图所示.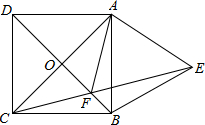 已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.
已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.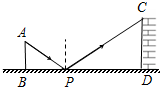 如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )
如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )