题目内容
10.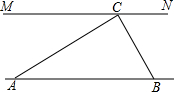 为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)
分析 如图,过点C作CD⊥AB于点D,通过解直角△ACD和直角△BCD来求CD的长度.
解答 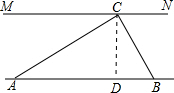 解:如图,过点C作CD⊥AB于点D,
解:如图,过点C作CD⊥AB于点D,
设CD=x.
∵在直角△ACD中,∠CAD=30°,
∴AD=$\frac{CD}{tan30°}$=$\sqrt{3}$x.
同理,在直角△BCD中,BD=$\frac{CD}{tan60°}$=$\frac{\sqrt{3}}{3}$x.
又∵AB=30米,
∴AD+BD=30米,即$\sqrt{3}$x+$\frac{\sqrt{3}}{3}$x=30.
解得x=13.
答:河的宽度的13米.
点评 本题考查了解直角三角形的应用.关键把实际问题转化为数学问题加以计算.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
20.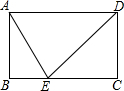 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 12 |
1. 如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
 如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
15. 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )| A. | 4 | B. | -2 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
2.下列计算正确的是( )
| A. | 22=4 | B. | 20=0 | C. | 2-1=-2 | D. | $\sqrt{4}$=±2 |
 如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.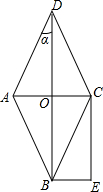 如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.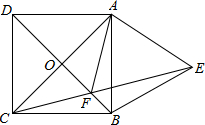 已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.
已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.