题目内容
17.(1)先化简,再求代数式的值($\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$)÷$\frac{a}{a+1}$,其中a=(-1)2012+tan60°.(2)关于x的方程3x2+mx-8=0有一个根是$\frac{2}{3}$,求另一个根及m的值.
分析 (1)先化简原式,然后将a的值化简即可求出答案.
(2)根据根与系数的关系即可求出m的值.
解答 解:(1)a=1+$\sqrt{3}$,
∴原式=$\frac{2}{a+1}$×$\frac{a+1}{a}$+$\frac{a+2}{(a+1)(a-1)}$×$\frac{a+1}{a}$
=$\frac{2}{a}$+$\frac{a+2}{a(a-1)}$
=$\frac{3}{a-1}$
=$\frac{3}{\sqrt{3}}$
=$\sqrt{3}$
(2)设另外一根为x,
由根与系数的关系可知:$\frac{2}{3}$x=-$\frac{8}{3}$,
∴x=-4,
∴-4+$\frac{2}{3}$=-$\frac{m}{3}$,
∴m=10
点评 本题考查学生的计算能力,解题的关键是熟练运用分式的运算法则以及根与系数的关系,本题属于基础题型

练习册系列答案
相关题目
19.某校初三参加体育测试,一组10人的引体向上成绩如下表:
这组同学引体向上个数的众数与中位数依次是( )
| 完成引体向上的个数 | 7 | 8 | 9 | 10 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 9.5和10 | B. | 9和10 | C. | 10和9.5 | D. | 10和9 |
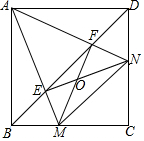 如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.
如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.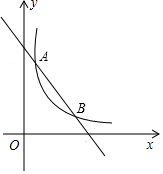 已知直线l:y=-x+5与双曲线y=$\frac{k}{x}$的图象交于A,B两点,且AB=3$\sqrt{2}$.
已知直线l:y=-x+5与双曲线y=$\frac{k}{x}$的图象交于A,B两点,且AB=3$\sqrt{2}$.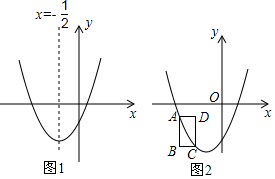
 如图,延长平行四边形ABCD的边AD,AB.作CE⊥AB交AB的延长线于点E,作CF⊥AD交AD的延长线于点F,若CE=CF.
如图,延长平行四边形ABCD的边AD,AB.作CE⊥AB交AB的延长线于点E,作CF⊥AD交AD的延长线于点F,若CE=CF.