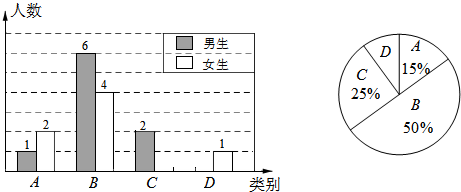
题目内容
5.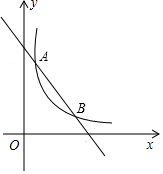 已知直线l:y=-x+5与双曲线y=$\frac{k}{x}$的图象交于A,B两点,且AB=3$\sqrt{2}$.
已知直线l:y=-x+5与双曲线y=$\frac{k}{x}$的图象交于A,B两点,且AB=3$\sqrt{2}$.(1)求双曲线的解析式;
(2)将直线l平移得y=-x+b,当平移后的直线与双曲线没有公共点时,直接写出b的取值范围.
(3)直线x=t(t>0)交双曲线于M,交线段AB于N,求△OMN面积的最大值.
分析 (1)化简方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{k}{x}}\end{array}\right.$,得到x2-5x+k=0,于是得到xA+xB=5,xA•xB=k,根据AB的长度列方程即可得到结论;
(2)根据题意列方程即可得到结论;
(3)根据题意设M(t,$\frac{11}{2t}$),N(t,-t+5),根据二次函数的性质即可得到结论;
解答 解:(1)解$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{k}{x}}\end{array}\right.$,
∴k=-x2+5x,
∴x2-5x+k=0,
∴xA+xB=5,xA•xB=k,(xB-xA)2=(xB+xA)2-4xAxB=25-4k,
AB2=(xA-xB)2+(yA-yB)2=(xA-xB)2+(5-xA+xB-5)2=2(xB-xA)2=2(25-4k)=(3$\sqrt{2}$)2=18,
∴k=4,
∴y=$\frac{4}{x}$;
(2)由题意得直线l向下平移,-x+b=$\frac{4}{x}$,化简为:-x2+bx-4=0,
∵平移后的直线与双曲线没有公共点,
∴△=b2-4×4<0,
∴|b|<4;
(3)∵直线x=t(t>0)交双曲线于M,交线段AB于N,
∴MN∥y轴,
设M(t,$\frac{4}{t}$),N(t,-t+5),
∴S△OMN=$\frac{1}{2}$×(-t+5-$\frac{4}{t}$)•t=-$\frac{1}{2}$(t-$\frac{5}{2}$)2+$\frac{9}{8}$,
∴△OMN面积的最大值是$\frac{8}{9}$.
点评 本题考查了一次函数与反比例函数的交点问题,正确的理解题意是解题的关键.

| A. | 4x-x=2x | B. | 2x•x4=x5 | C. | x2y÷y=x2 | D. | (-3x)3=-9x3 |
 如图,BE,CF分别是△ABC的高,M为BC的中点,EF=5,BC=10,则△EFM的周长是( )
如图,BE,CF分别是△ABC的高,M为BC的中点,EF=5,BC=10,则△EFM的周长是( )| A. | 21 | B. | 18 | C. | 13 | D. | 15 |
| A. | 1.2×109 | B. | 1.2×108 | C. | 12×109 | D. | 12×108 |