题目内容
11.已知函数y=$\left\{\begin{array}{l}{-(x-1)^{2}+1(x≤3)}\\{-(x-5)^{2}+1(x>3)}\end{array}\right.$,(1)若使y=k成立的k值恰好有三个,则k=-3;
(2)若使y=k成立的x值恰好有两个,则k的取值范围为k=1或k<-3.
A、0 B、1 C.2 D、3.
分析 首先在坐标系中画出已知函数y=$\left\{\begin{array}{l}{-(x-1)^{2}+1(x≤3)}\\{-(x-5)^{2}+1(x>3)}\end{array}\right.$的图象,然后利用数形结合的方法即可求解.
解答 解:函数y=$\left\{\begin{array}{l}{-(x-1)^{2}+1(x≤3)}\\{-(x-5)^{2}+1(x>3)}\end{array}\right.$的图象如图:
(1)根据图象知道当y=-3时,对应成立的x有恰好有3个,
所以k=-3;
(2)根据图象知道当y=1或y<-3时,对应成立的x有恰好有2个,
所以k=1或k<-3.
故答案为:k=-3;k=1或k<-3
点评 此题主要考查了利用二次函数的图象解决交点问题,解题的关键是把解方程的问题转换为根据函数图象找交点的问题.

练习册系列答案
相关题目
2.已知①x=1;②x2-2x=0;③x-3=5;④6-x;⑤2x+y=3;⑥xy=2,其中一元一次方程有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.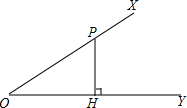 如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
 如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )| A. | 与点P的位置有关 | B. | 与PH的长度有关 | ||
| C. | 与∠XOY的大小有关 | D. | 与点P的位置和∠XOY的大小都无关 |