题目内容
7.如图,在三角形ABC中,点O是AC边上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠ACD的平分线于点F.(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF会变成矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,AB与EC相交于点P,与EF相交于点D,若BC=2,AE=$\sqrt{6}$,求BP的长.
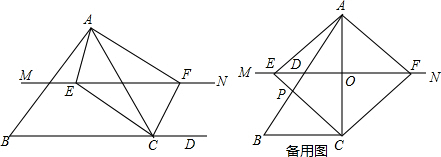
分析 (1)直接利用平行线的性质结合结合角平分线的性质得出∠OCE=∠BCE,∠OCF=∠GCF,即可得出EO=CO,FO=CO求出答案即可;
(2)利用已知得出AO+CO=EO+FO,即AC=EF,进而利用矩形的判定方法得出答案;
(3)利用正方形的性质得出∠ACB=90°,OE∥BC,进而得出△BPC∽△DAF,△BPC∽△DAF,再利用相似三角形的性质得出答案.
解答 证明:(1)∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.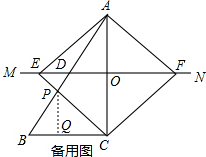 ∵当点O运动到AC的中点时,AO=CO,
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,∴四边形AECF是平行四边形,
∵FO=CO,∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
(3)解:如备用图:设AB与EF交于点D,过点P作PQ⊥BC于点Q,
当四边形AECF是正方形时,
∵AE=EC=AF=$\sqrt{6}$,∠AEC=∠ECF=90°,∠AOC=90°,AO=OC,
∴∠ACE=∠BCE=∠AFE=45°,AC=$\sqrt{6+6}=2\sqrt{3}$,
∴∠ACB=90°,OE∥BC,
∴∠ADO=∠ABC,
∴△BPC∽△DAF
而BC=2,
∴tan∠B=$\frac{AC}{BC}=\frac{{2\sqrt{3}}}{2}=\sqrt{3}$,
∴∠B=60°,∠BAC=30°,
∴AB=2BC=4,AD=$\frac{1}{2}$AB=2
设BQ=x,则,BP=2x,CQ=PQ=2-x,
而△BPC∽△DAF,$\frac{PC}{PB}=\frac{AF}{AD}=\frac{{\sqrt{6}}}{2}$,
∴PC=$\sqrt{6}$x,
在Rt△PQC中,PQ2+CQ2=PC2,
得$2(2-x{)^2}={(\sqrt{6}x)^2}$,
解得${x_1}=\sqrt{3}-1,{x_2}=-\sqrt{3}-1$(不合题意,舍去)
∴BP=2BQ=$2\sqrt{3}-2$.
点评 此题主要考查了四边形综合以及相似三角形的判定与性质和矩形的判定以及正方形的性质等知识,正确掌握矩形的判定与正方形的性质是解题关键.

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案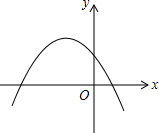 已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | m>$\frac{2}{3}$ | B. | m>$\frac{1}{2}$ | C. | m<$\frac{1}{2}$ | D. | m<$\frac{2}{3}$ |
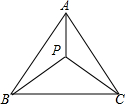 如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.
如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.