题目内容
10．
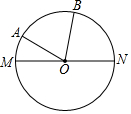在半径为1的⊙O中，MN是直径，∠AOM=27°，∠BOA=66°，在直径MN上有一点C，AC+BC的和最小，则这个最小值等于$\sqrt{3}$．
分析 直接利用轴对称求最短路线的方法得出A点关于MN的对称点，进而求出答案．
解答 
解：作A点关于MN的对称点A′，过点OD⊥A′B于点D，
∵∠AOM=27°，∠BOA=66°，
∴∠MOA′=27°，则∠A′OB=120°，
∵A′O=BO，
∴∠A′OD=∠BOD=60°，
∴∠DA′O=30°，
∵A′O=1，
∴DO=$\frac{1}{2}$，
∴A′D=$\frac{\sqrt{3}}{2}$，
∴A′B=$\sqrt{3}$．
故AC+BC的和最小值等于$\sqrt{3}$．
故答案为：$\sqrt{3}$．
点评 此题主要考查了利用轴对称求最短路线以及解直角三角形，正确找出C点位置是解题关键．
练习册系列答案
相关题目
5．圆柱的体积V、高h、底面圆的半径R之间的解析式是V=πR2h，已知V=50cm3，填写下表：
（1）变量h是变量R的函数吗？
（2）变量h是变量R的反比例函数吗？
| R（cm） | 1 | 2 | 3 | 4 | 5 | 6 |
| h（cm） | $\frac{50}{π}$ | $\frac{25}{2π}$ | $\frac{50}{9π}$ | $\frac{25}{8π}$ | $\frac{2}{π}$ | $\frac{25}{8π}$ |
（2）变量h是变量R的反比例函数吗？
15．在线段AB上取一点C，使AC=$\frac{1}{3}$AB，再在线段AB的延长线上取一点D，使DB=$\frac{1}{4}$AD，则线段BC的长度是线段DC长度的（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |
如图，点C分线段AB为2：1两部分，D点为线段CB的中点，AD=5，求线段AB的长．
19．$\sqrt{32}$的整数部分是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
对数轴上的点P进行如下操作：先把点P表示的数乘以-2，再把所得数对应的点向左运动一个单位，得到点P的对应点P1．