题目内容
1.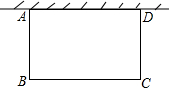 如图,某居民小区要在一块一边靠墙(墙长15m)的高地上修建一个矩形花园ABCD,花园的一边靠墙,另外三边用总长为40m的栅栏围成.则BC=15米时,花园的面积最大,最大面积是187.5平方米.
如图,某居民小区要在一块一边靠墙(墙长15m)的高地上修建一个矩形花园ABCD,花园的一边靠墙,另外三边用总长为40m的栅栏围成.则BC=15米时,花园的面积最大,最大面积是187.5平方米.
分析 首先根据矩形的性质,由花园的BC边长为x(m),可得AB的长,然后根据矩形面积的求解方法,即可求得y与x之间的函数关系式,根据二次函数的增减性,可知当x<20时,y随x的增大而增大,故可得当x=15时,y最大,将其代入函数解析式,即可求得最大面积.
解答 解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
∵BC=xm,AB+BC+CD=40m,
∴AB=$\frac{40--x}{2}$m,
∴花园的面积为:y=x•$\frac{40-x}{2}$=-$\frac{1}{2}$x2+20x(0<x≤15);
∴y与x之间的函数关系式为:y=-$\frac{1}{2}$x2+20x(0<x≤15);
∵y=-$\frac{1}{2}$x2+20x=-$\frac{1}{2}$(x-20)2+200,
∵a=-$\frac{1}{2}$<0,
∴当x<20时,y随x的增大而增大,
∴当x=15时,y最大,最大值y=187.5平方米.
∴当BC=15米时,花园的面积最大,最大面积为187.5平方米;
故答案为:15,187.5.
点评 此题考查了二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,能根据题意求得函数解析式,然后根据二次函数的性质求解.

练习册系列答案
相关题目
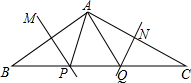 如图,在△ABC中,∠BAC=120°,如果PM、QN分别垂直平分AB、AC,那么∠PAQ=60°,若BC=10cm,则△APQ的周长为10cm.
如图,在△ABC中,∠BAC=120°,如果PM、QN分别垂直平分AB、AC,那么∠PAQ=60°,若BC=10cm,则△APQ的周长为10cm.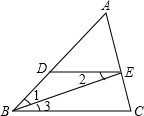 已和,如图,BE平分∠ABC,∠1=∠2,请说明∠AED=∠C.根据提示填空.
已和,如图,BE平分∠ABC,∠1=∠2,请说明∠AED=∠C.根据提示填空.