题目内容
14.(1)计算:($\frac{1}{2}$)-2-$\sqrt{12}$÷2-|$\sqrt{3}$-2|;(2)先化简,再选择一个使原式有意义的x代入求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{x}$.
分析 (1)直接利用负指数幂的性质结合二次根式的性质、绝对值的性质化简,进而求出答案;
(2)首先将括号里面通分,进而利用分式乘除运算法则化简求出答案.
解答 解:(1)($\frac{1}{2}$)-2-$\sqrt{12}$÷2-|$\sqrt{3}$-2|
=4-2$\sqrt{3}$÷2-(2-$\sqrt{3}$)
=4-$\sqrt{3}$-2+$\sqrt{3}$
=2;
(2)(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{x}$
=$\frac{x-1}{x}$×$\frac{x}{(x-1)^{2}}$
=$\frac{1}{x-1}$,
当x=2时,原式=$\frac{1}{2-1}$=1.
点评 此题主要考查了分式的化简求值以及实数运算,正确化简分式是解题关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,将△ABC点C顺时针旋转90°后得则△A′B′C′.
如图,在平面直角坐标系中,将△ABC点C顺时针旋转90°后得则△A′B′C′. 已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别等于2cm,2cm,2cm.
已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别等于2cm,2cm,2cm.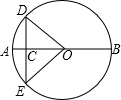 如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若∠AOD=40°,求$\widehat{BD}$,$\widehat{AE}$的度数.
如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若∠AOD=40°,求$\widehat{BD}$,$\widehat{AE}$的度数.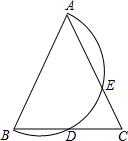 已知:如图,在△ABC中,AB=AC,以腰AB为直径作半圆O,分别交BC,AC于点D,E.
已知:如图,在△ABC中,AB=AC,以腰AB为直径作半圆O,分别交BC,AC于点D,E.