题目内容
13.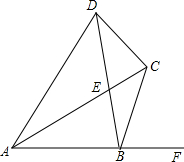 已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.
已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.
分析 先证明A、B、C、D四点共圆,由圆周角定理得出∠ABD=∠ACD,再由已知条件和圆内接四边形的性质得出∠ACD=∠ADC,由三角形内角和定理求出∠ACD=∠ADC=75°,得出∠ACB=45°,作BM⊥AC于M,则∠AMB=∠CMB=90°,由含30°角的直角三角形的性质和勾股定理得出BM=$\frac{1}{2}$AB=1,AM=$\sqrt{3}$,得出△CBM是等腰直角三角形,因此CM=BM=1,即可得出AC的长.
解答 解:∵∠DAB+∠DCB=180°,
∴A、B、C、D四点共圆,∠DAB=180°-∠DCB=60°,
∴∠ABD=∠ACD,
∵∠ABD=∠CBF,
∴∠ACD=∠CBF,
∵∠CBF=∠ADC,
∴∠ACD=∠ADC,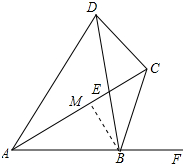
∵AC平分∠DAB,
∴∠DAC=∠BAC=30°,
∴∠ACD=∠ADC=75°,
∴∠ACB=120°-75°=45°,
作BM⊥AC于M,如图所示:
则∠AMB=∠CMB=90°,
∴BM=$\frac{1}{2}$AB=1,△CBM是等腰直角三角形,
∴AM=$\sqrt{3}$BM=$\sqrt{3}$,CM=BM=1,
∴AC=AM+CM=$\sqrt{3}$+1;
故答案为:$\sqrt{3}$+1.
点评 本题是四点共圆综合题目,考查了四点共圆、圆周角定理、三角形内角和定理、圆内接四边形的性质、含30°角的直角三角形的性质、勾股定理、等腰直角三角形的判定与性质等知识;本题综合性强,有一定难度,证明四点共圆和作辅助线运用特殊直角三角形的性质是解决问题的关键.

练习册系列答案
相关题目
4.用配方法解方程x2+4x+1=0,则配方正确的是( )
| A. | (x+2)2=3 | B. | (x+2)2=-5 | C. | (x+2)2=-3 | D. | (x+4)2=3 |
2.亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会,并在会上投票选出2022年第19届亚运会举办城市为杭州.5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2015年9月16日20时应是( )


| A. | 伦敦时间2015年9月16日11时 | B. | 巴黎时间2015年9月16日13时 | ||
| C. | 智利时间2015年9月16日5时 | D. | 曼谷时间2015年9月16日18时 |
 实数a,b,c在数轴上对应点的位置如图所示,则$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|=a-2b.
实数a,b,c在数轴上对应点的位置如图所示,则$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|=a-2b. .
.
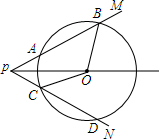 如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.
如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC. 圆柱和棱柱有很多相同点,下面的这个几何体也有这样的相同点吗?
圆柱和棱柱有很多相同点,下面的这个几何体也有这样的相同点吗?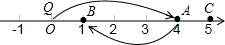 如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.
如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.