题目内容
10.某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价和售价如下表:| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)应如何进货,使销售完节能灯时,商场获得的利润恰好是进货价的30%,此时利润为多少?
分析 (1)设甲种节能灯购进x只,则乙种节能灯购进(1200-x)只,根据甲型、乙型的进货价格列出方程,再进行求解即可;
(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200-a)只,由题意可得:甲型的总利润+乙型的总利润=总进货款×30%,根据等量关系列出方程,再解即可.
解答 解:(1)设甲种节能灯购进x只,乙种节能灯购进(1200-x)只,
依题意得,25x+45(1200-x)=46000,
解得:x=400,
则1200-x=800(只),
答:甲种节能灯购进400只,乙种节能灯购进800只,进货款恰好为46000元;
(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200-a)只,
由题意,得:(30-25)a+(60-45)(1200-a)=[25a+45(1200-a)]×30%.
解得:a=450.
购进乙型节能灯1200-450=750只.
5a+15(1200-a)=13500元.
答:商场购进甲型节能灯450只,购进乙型节能灯750只时利润为13500元.
点评 此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.

练习册系列答案
相关题目
20.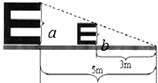 根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
 根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )| A. | 1.44cm | B. | 2.16cm | C. | 2.4cm | D. | 3.6cm |
5.下面几个有理数中,最小的数是( )
| A. | 1 | B. | -2 | C. | 0 | D. | -2.5 |
15.若分式$\frac{x-1}{x-3}$有意义,则x满足的条件是( )
| A. | x=1 | B. | x=3 | C. | x≠1 | D. | x≠3 |
2.计算:-4+3=( )
| A. | 1 | B. | -5 | C. | -1 | D. | -6 |
20.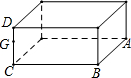 如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )
如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )
 如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )
如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )| A. | 6cm | B. | $4+\sqrt{89}$cm | C. | 13cm | D. | 17cm |
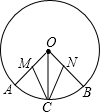 已知如图所示,OA、OB、OC是⊙O的三条半径,弧AC和弧BC相等,M、N分别是OA、OB的中点.求证:MC=NC.
已知如图所示,OA、OB、OC是⊙O的三条半径,弧AC和弧BC相等,M、N分别是OA、OB的中点.求证:MC=NC.