题目内容
7.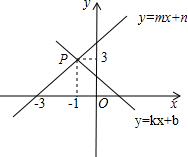 如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.
如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.
分析 利用函数图象,找出在x轴上方,且直线y=mx+n在直线y=kx+b下方所对应的自变量的范围即可.
解答 解:利用函数图象得,当x≥-3时,mx+n≥0,
当x<-1时,mx+n<kx+b,
所以不等式组0≤mx+n<kx+b的解集为-3≤x<-1.
故答案为-3≤x<-1.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )
如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )
 如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )
如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )| A. | 52° | B. | 62° | C. | 64° | D. | 72° |
15.已知抛物线y=x2-(2m+1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是( )
| A. | 0≤m≤1.5 | B. | m≥1.5 | C. | 0≤m≤1 | D. | 0<m≤1.5 |
19.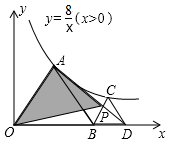 如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
 如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 8 |
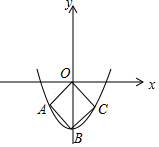 如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.
如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.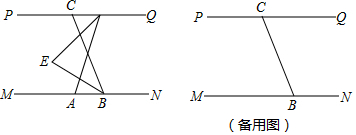
 如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(-2,2),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第2018次跳动至点A2018的坐标是(1010,1009).
如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(-2,2),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第2018次跳动至点A2018的坐标是(1010,1009).