题目内容
19.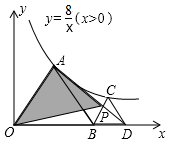 如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 8 |
分析 如图,作AH⊥BC于H.由△OAB是等边三角形,可知∠AOH=60°,AH=$\sqrt{3}$OH,设OH=a,则AH=$\sqrt{3}$a,推出A(a,$\sqrt{3}$a),把A的坐标代入y=$\frac{8}{x}$,得到a2=$\frac{8}{3}$$\sqrt{3}$,由△BCD也是等边三角形,推出∠CBD=∠AOB=60°,推出OA∥BC,推出S△AOP=S△AOB,求出△AOB的面积即可解决问题.
解答 解:如图,作AH⊥BC于H.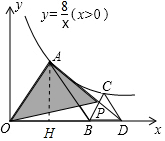
∵△OAB是等边三角形,
∴∠AOH=60°,AH=$\sqrt{3}$OH,设OH=a,则AH=$\sqrt{3}$a,
∴A(a,$\sqrt{3}$a),把A的坐标代入y=$\frac{8}{x}$,得到a2=$\frac{8}{3}$$\sqrt{3}$,
∵△BCD也是等边三角形,
∴∠CBD=∠AOB=60°,
∴OA∥BC,
∴S△AOP=S△AOB=$\frac{1}{2}$•OB•AH=$\frac{1}{2}$•2a•$\sqrt{3}$a=$\sqrt{3}$a2=8,
故选D.
点评 本题考查反比例函数的k的几何意义,等边三角形的性质,直角三角形30度角的性质、平行线的性质、等高模型等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考填空题中的压轴题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
19.下列各图中,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
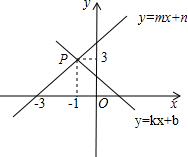 如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.
如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.



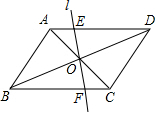 在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.
在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$. 请将下列证明过程补充完整:
请将下列证明过程补充完整: 如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(1,-1).
如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(1,-1).