题目内容
2.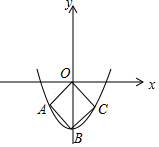 如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.
如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.
分析 连接AC交OB于点D,根据正方形的性质得出点A坐标为($\frac{c}{2}$,$\frac{c}{2}$),代入解析式即可求得c的值.
解答 解:如图,连接AC交OB于点D,
∵OB=c,
∴OD=AD=$\frac{c}{2}$,∠ADO=90°,
则点A的坐标为($\frac{c}{2}$,$\frac{c}{2}$),
代入抛物线y=$\frac{1}{2}$x2+c得:$\frac{{c}^{2}}{8}$+c=$\frac{c}{2}$,
解得:c=0(舍)或c=-4,
故答案为:-4.
点评 本题主要考查二次函数图象上点的坐标特点及正方形的性质,根据正方形的得出点A的坐标是解题的关键.

练习册系列答案
相关题目
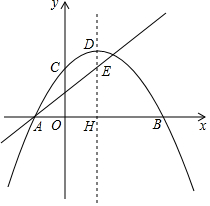 已知:如图,抛物线y=-$\frac{1}{4}$(x-h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=$\frac{3}{4}$x+$\frac{3}{2}$经过点A与对称轴交于E,点E的纵坐标为3.
已知:如图,抛物线y=-$\frac{1}{4}$(x-h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=$\frac{3}{4}$x+$\frac{3}{2}$经过点A与对称轴交于E,点E的纵坐标为3.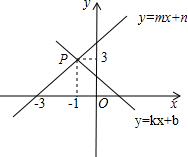 如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.
如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.



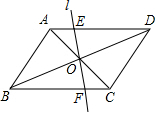 在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.
在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.