题目内容
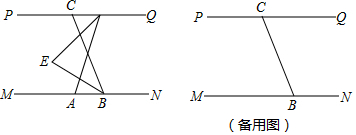
16.如图,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE,BE交于点E,∠CBN=120°.(1)若∠ADQ=110°,求∠BED的度数;
(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示)
分析 (1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分两种情形讨论即可解决问题.
解答 解:(1)如图1中,延长DE交MN于H.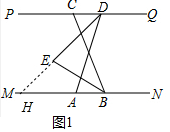
∵∠ADQ=110°,ED平分∠ADP,
∴∠PDH=$\frac{1}{2}$∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB平分∠ABC,
∴∠EBH=$\frac{1}{2}$∠ABC=30°,
∴∠BED=∠EHB+∠EBH=75°.
(2)有两种情形,如图2中,当n>60°.延长DE交MN于H.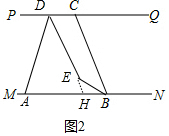
∵PQ∥MN,
∴∠QDH=∠DHB=$\frac{1}{2}$n,
∴∠BED=∠EHB+∠EBH=($\frac{1}{2}$n)°+30°,
当n<60°,如图3中,设BE交PQ于H.
∵∠DHB=∠HBA=30°,∠EDH=($\frac{1}{2}$n)°,
又∵∠DHB=∠BED+∠EDH,
∴∠BED=30°-($\frac{1}{2}$n)°,
当n=60°,∠BED不存在.
综上所述,∠BED=($\frac{1}{2}$n)°+30°或30°-($\frac{1}{2}$n)°.
点评 本题考查平行线的性质、角平分线的定义、三角形的外角的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
6.甲、乙两名同学学期的四次数学测试成绩(单位:分)如下表:
据上标计算,甲、乙两名同学四次数学测试成绩的方差分别为S2甲=17,S2乙=25,下列说法:①甲同学四次数学测试成绩的平均数是90分;②甲同学四次数学测试成绩的中位数是90分;③乙同学四次数学测试成绩的众数是80分;④乙同学四次数学测试成绩较稳定,其中正确的有( )
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 甲 | 87 | 95 | 85 | 93 |
| 乙 | 80 | 80 | 90 | 90 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 若实数a满足|a-$\frac{1}{2}$|=$\frac{3}{2}$,则a对应于图中数轴上的点可以是A、B、C三点中的点B.
若实数a满足|a-$\frac{1}{2}$|=$\frac{3}{2}$,则a对应于图中数轴上的点可以是A、B、C三点中的点B.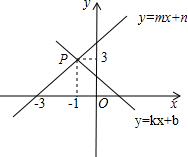 如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.
如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0≤mx+n<kx+b的解集是-3≤x<-1.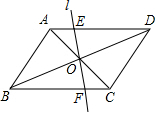 在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.
在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.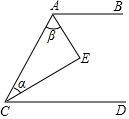 请将下列证明过程补充完整:
请将下列证明过程补充完整: