题目内容
14. 如图,△ABC中,∠C=90°,且BC=5,它的内切⊙O分别与边AB、BC、CA相切于点D、F、E,⊙O的半径r=2.求△ABC的周长.
如图,△ABC中,∠C=90°,且BC=5,它的内切⊙O分别与边AB、BC、CA相切于点D、F、E,⊙O的半径r=2.求△ABC的周长.
分析 连接OF、OE.先证明四边形OECF是正方形,从而可求得BF=DB=3,设AD=AE=x,最后再Rt△ABC中,由勾股定理列方程求解可求得x=10,从而可求得△ABC的周长.
解答 解:如图所示:连接OF、OE.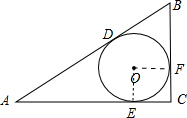
∵BC是圆O的切线,
∴OF⊥BC.
同理:OE⊥AC.
∴∠OFC=∠C=∠OEC=90°.
∴四边形OECF是矩形.
∵OF=OE,
∴四边形OECF是正方形.
∴FC=EC=2.
∴BF=3.
由切线长定理可知:DB=BF=3,AD=AE.
设AD=AE=x,则AC=x+2,AB=x+3.
在Rt△ABC中,由勾股定理得:AB2=AC2+BC2,(x+3)2=(x+2)2+52.
解得:x=10.
∴AC=10+2=12,AB=10+3=13.
∴△ABC的周长=12+13+5=30.
点评 本题主要考查的是三角形的内切圆,正方形的性质和判定、切线长定理,证得四边形OECF是正方形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在下列所给出坐标的点中,在第二象限的是( )
| A. | (1,-3) | B. | (-2,3) | C. | (3,4) | D. | (-1,-2) |
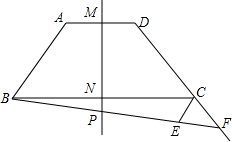 已知等腰梯形ABCD中,AD∥BC,AD=4,BC=10,AB=CD=5,直线MN是等腰梯形的对称轴,P是射线MN上一点,射线BP交射线DC于点F,过C点作CE∥AB,与射线BP交于点E.
已知等腰梯形ABCD中,AD∥BC,AD=4,BC=10,AB=CD=5,直线MN是等腰梯形的对称轴,P是射线MN上一点,射线BP交射线DC于点F,过C点作CE∥AB,与射线BP交于点E.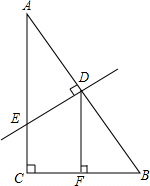 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB、AC于点D、E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB、AC于点D、E.