题目内容
6.已知关于x的二次函数y=x2-(a-1)x-a+1的图象与x轴有且只有一个公共点,求a的值,并求出公共点的坐标.分析 由二次函数的图象与x轴有且只有一个公共点,得出△=a2-2a-3=0,解方程得出a的值,再把a的值代入二次函数解析式,即可得出公共点即顶点的坐标.
解答 解:∵二次函数y=x2-(a-1)x-a+1的图象与x轴有且只有一个公共点,
∴△=[-(a-1)]2-4×1×(-a+1)=a2-2a-3=0,
解得:a=1,或a=-3,
当a=1时,y=x2,
公共点即为顶点,坐标为(0,0);
当a=-3时,y=x2+4x+4=(x+2)2,
公共点即为顶点,坐标为(-2,0).
点评 本题考查了二次函数的图象与x轴的交点、判别式、解方程、抛物线的顶点坐标;本题难度适中,由判别式求出a的值是解决问题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
1.方程2-$\frac{2x-4}{3}$=-$\frac{x-7}{6}$去分母得( )
| A. | 2-2(2x-4)=-(x-7) | B. | 12-2(2x-4)=-x-7 | C. | 12-2(2x-4)=-(x-7) | D. | 以上答案均不对 |
11.一元二次方程2x2+6x=9的二次项系数、一次项系数、常数项分别是( )
| A. | 2,6,9 | B. | 6,2,9 | C. | 2,6,-9 | D. | 6,2,-9 |
 如图,△ABC中,∠C=90°,且BC=5,它的内切⊙O分别与边AB、BC、CA相切于点D、F、E,⊙O的半径r=2.求△ABC的周长.
如图,△ABC中,∠C=90°,且BC=5,它的内切⊙O分别与边AB、BC、CA相切于点D、F、E,⊙O的半径r=2.求△ABC的周长.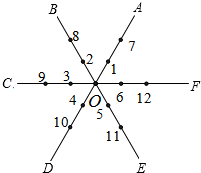 如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字 1,2,3,4,5,6,7,…
如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字 1,2,3,4,5,6,7,…