题目内容
9.解下列不等式组,并把解集表示在数轴上(1)$\frac{1-x}{3}$$≤\frac{1-2x}{7}$
(2)$\left\{\begin{array}{l}{3x-4>2(x-2)}\\{\frac{3x-2}{5}-\frac{2x+1}{3}≥-1}\end{array}\right.$.
分析 (1)先去分母,再去括号、移项合并得到-x≤-4,然后把x的系数化为1即可;
(2)先分别解两个不等式得到x>0和x≤4,再根据大小小大中间找确定不等式组的解集,然后利用数轴表示解集.
解答 解:(1)去分母得7(1-x)≤3(1-2x),
去括号得7-7x≤3-6x,
移项得-7x+6x≤3-7,
合并得-x≤-4;
系数化为1得x≥4,
用数轴表示为:
(2)$\left\{\begin{array}{l}{3x-4>2(x-2)①}\\{\frac{3x-2}{5}-\frac{2x+1}{3}≥-1②}\end{array}\right.$,
解①得x>0,
解②得x≤4,
所以不等式组的解为0<x≤4,
用数轴表示为: .
.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.也考查了解一元一次不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在自然数范围内,方程2x+y=7的解有( )
| A. | 一组 | B. | 三组 | C. | 四组 | D. | 无数组 |
1.方程2-$\frac{2x-4}{3}$=-$\frac{x-7}{6}$去分母得( )
| A. | 2-2(2x-4)=-(x-7) | B. | 12-2(2x-4)=-x-7 | C. | 12-2(2x-4)=-(x-7) | D. | 以上答案均不对 |

 如图,直线MN与直线AB、CD相交于M、N,∠3=∠4,求证:∠1=∠2.
如图,直线MN与直线AB、CD相交于M、N,∠3=∠4,求证:∠1=∠2. 如图,△ABC中,∠C=90°,且BC=5,它的内切⊙O分别与边AB、BC、CA相切于点D、F、E,⊙O的半径r=2.求△ABC的周长.
如图,△ABC中,∠C=90°,且BC=5,它的内切⊙O分别与边AB、BC、CA相切于点D、F、E,⊙O的半径r=2.求△ABC的周长.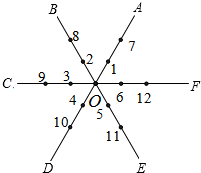 如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字 1,2,3,4,5,6,7,…
如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字 1,2,3,4,5,6,7,…