题目内容
11.符号“f”表示一种运算,它对一些数的运算如下:f(1)=1+$\frac{2}{1}$,f(2)=1+$\frac{2}{2}$,f(3)=1+$\frac{2}{3}$,f(4)=1+$\frac{2}{4}$…(1)利用以上运算的规律写出f(n)=1+$\frac{2}{n}$;(n为正整数)
(2)计算:f(1)•f(2)•f(3)•…•f(100)的值.
分析 (1)根据f(1)、f(2)、f(3)、f(4)的运算方法,写出f(n)的表达式即可.
(2)根据(1)中求出的f(n)的表达式,求出f(1)•f(2)•f(3)•…•f(100)的值是多少即可.
解答 解:(1)∵f(1)=1+$\frac{2}{1}$,f(2)=1+$\frac{2}{2}$,f(3)=1+$\frac{2}{3}$,f(4)=1+$\frac{2}{4}$…
∴f(n)=1+$\frac{2}{n}$.
(2)f(1)•f(2)•f(3)•…•f(100)
=(1+$\frac{2}{1}$)(1+$\frac{2}{2}$)(1+$\frac{2}{3}$)(1+$\frac{2}{4}$)…(1+$\frac{2}{100}$)
=$\frac{3}{1}$×$\frac{4}{2}$×$\frac{5}{3}$×$\frac{6}{4}$×…×$\frac{102}{100}$
=$\frac{101×102}{1×2}$
=5151
故答案为:1+$\frac{2}{n}$.
点评 此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

练习册系列答案
相关题目
16.若“?”是某种新规定的运算符号,设a?b=3a+2b,则[(x+y)?(x-y)]?3x化简为( )
| A. | 0 | B. | 21x+3y | C. | 5x | D. | 9x+6y |
 如图,AB与⊙O相切于点B,AO及AO的延长线分别交⊙O于D、C两点,若∠A=40°,求∠C的度数.
如图,AB与⊙O相切于点B,AO及AO的延长线分别交⊙O于D、C两点,若∠A=40°,求∠C的度数. 如图所示,已知点E是四边形ABCD内的一点,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,试说明AD与BC的位置关系.
如图所示,已知点E是四边形ABCD内的一点,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,试说明AD与BC的位置关系.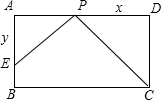 已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE⊥CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE⊥CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并写出x的取值范围. 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是$\frac{21}{2}$.
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是$\frac{21}{2}$.