题目内容
6.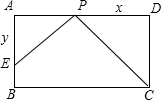 已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE⊥CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE⊥CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
分析 只要证明△AEP∽△DPC,得$\frac{AE}{DP}$=$\frac{AP}{DC}$,可得y=-$\frac{1}{2}$x2+$\frac{3}{2}$x,利用配方法求出x取何值时,y的最大值,结合题意可得x的取值范围.
解答 解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠EPC=90°,
∴∠AEP+∠APE=90°,∠AEP+∠DPC=90°,
∴∠AEP=∠DPC,
∴△AEP∽△DPC,
∴$\frac{AE}{DP}$=$\frac{AP}{DC}$,
∴$\frac{y}{x}$=$\frac{3-x}{2}$,
∴y=-$\frac{1}{2}$x2+$\frac{3}{2}$x.
∵y=-$\frac{1}{2}$x2+$\frac{3}{2}$x=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{9}{8}$,
∴x=$\frac{3}{2}$时y的最大值为$\frac{9}{8}$,
∵$\frac{9}{8}$<2,
∴x的取值范围为0<x<3.
∴y=-$\frac{1}{2}$x2+$\frac{3}{2}$x(0<x<3).
点评 本题考查相似三角形的判定和性质、矩形的性质等知识,解题的关键是灵活应用二次函数的性质解决自变量的取值范围,属于中考常考题型.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15.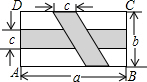 长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )
长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )
 长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )
长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )| A. | bc-ab+ac+c2 | B. | ab-bc-ac+c2 | C. | a2+ab+bc-ac | D. | b2-bc+a2-ab |
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).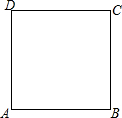 如图,边长为2的正方形ABCD,一点P从A点出发沿AB-BC以每秒1个单位速度运动到C点,设运动的时间为x秒,四边形APCD的面积为y.
如图,边长为2的正方形ABCD,一点P从A点出发沿AB-BC以每秒1个单位速度运动到C点,设运动的时间为x秒,四边形APCD的面积为y.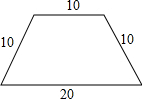 有一根围成梯形的篱笆,它的各边长如图所示,为了其他用处,将它改围成一个长方形篱笆,使得围成的长方形的一边长为10,则此时篱笆围成的长方形的另一边长为多少?若改围成一个正方形的篱笆,正方形的边长为多少?并比较围出的长方形和正方形哪个面积更大?
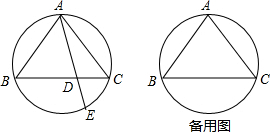
有一根围成梯形的篱笆,它的各边长如图所示,为了其他用处,将它改围成一个长方形篱笆,使得围成的长方形的一边长为10,则此时篱笆围成的长方形的另一边长为多少?若改围成一个正方形的篱笆,正方形的边长为多少?并比较围出的长方形和正方形哪个面积更大?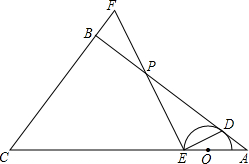 如图,在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,连接ED,过点E作ED的高,交射线AB于点P,交射线CB于点F.
如图,在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,连接ED,过点E作ED的高,交射线AB于点P,交射线CB于点F.