题目内容
8.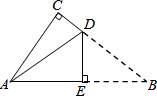 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 10cm |
分析 在Rt△ABC中,可求出AB的长度,根据折叠的性质可得出AE=EB=$\frac{1}{2}$AB.
解答 解:∵AC=6cm,BC=8cm,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10cm,
∵由折叠的性质得,∠B=∠DAE,DE⊥AB,
∴AE=EB=$\frac{1}{2}$AB=5cm.
故选B.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
4.某次知识竞赛共计25道题,评分标准如下:答对1题加4分,答错1题扣1分,她的总分为75分,则她答对了( )
| A. | 18题 | B. | 19题 | C. | 20题 | D. | 21题 |
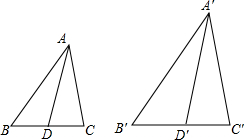 如图,D、D′分别是△ABC和△A′B′C′的边BC、B′C′的中点,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{AD}{A′D′}$,求证:△ABC∽△A′B′C′.
如图,D、D′分别是△ABC和△A′B′C′的边BC、B′C′的中点,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{AD}{A′D′}$,求证:△ABC∽△A′B′C′.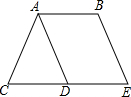 在平行四边形ABED中,CD为DE延长线,连接AC,AD恰好为∠BAC角平分线,且∠BAD=60°,BE=2cm,求△ACD的周长.
在平行四边形ABED中,CD为DE延长线,连接AC,AD恰好为∠BAC角平分线,且∠BAD=60°,BE=2cm,求△ACD的周长.